《2025年步步高精准讲练物理选择性必修第二册》

5. (多选)(2024·宁波市镇海中学高二期末)一匀强磁场的磁感应强度大小为$ B $,方向垂直于纸面向里,其边界如图中虚线所示,$ ab $为半径为$ R $的半圆,$ ac $、$ bd $与直径$ ab $共线,$ a $、$ c $间的距离等于半圆的半径$ R $。一束质量均为$ m $、电量均为$ q $的带负电的粒子,在纸面内从$ c $点垂直于$ ac $以不同速度射入磁场,不计粒子重力及粒子间的相互作用。下列说法正确的是

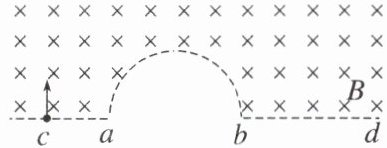
A.可以经过半圆形边界的粒子的速率最小值为$ \frac{qBR}{m} $
B.可以经过半圆形边界的粒子的速率最大值为$ \frac{3qBR}{2m} $
C.在磁场中运动时间最短的粒子速率为$ \frac{qBR}{2m} $
D.在磁场中运动时间最短的粒子运动时间为$ \frac{2\pi m}{3qB} $

答案：
5.BD [粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律有$qvB = m\frac{v^{2}}{R}$，解得粒子的轨迹半径$R=\frac{mv}{qB}$，粒子速度$v$越大，半径$R$越大。粒子在磁场中的运动轨迹如图所示，在能达到半圆形边界的粒子中，经过$a$点的粒子半径最小，速度最小，其轨迹如图中1所示，由$\frac{R}{2}=\frac{mv_{\min}}{qB}$
得$v_{\min}=\frac{qBR}{2m}$，故A错误;
经过$b$点的粒子半径最大，速度最大，其轨迹如图中2所示，由$\frac{3R}{2}=\frac{mv_{\max}}{qB}$，
解得$v_{\max}=\frac{3qBR}{2m}$，故B正确;
轨迹圆弧所对应的弦与$ab$半圆形边界相切时，圆心角最小，运动时间最短，其轨迹如图中3所示，圆心恰好位于$a$点，由$R=\frac{mv}{qB}$，
解得$v=\frac{qBR}{m}$，故C错误;粒子在磁场中做匀速圆周运动的周期$T=\frac{2\pi r}{v}=\frac{2\pi m}{qB}$，粒子在磁场中的最短运动时间为$t=\frac{T}{3}=\frac{2\pi m}{3qB}$，故D正确。]

6. (多选)如图所示,在Ⅰ、Ⅱ两个区域内存在磁感应强度大小均为$ B $的匀强磁场,磁场方向分别垂直于纸面向外和向里,$ AD $、$ AC $边界的夹角$ \angle DAC = 30^{\circ} $,边界$ AC $与边界$ MN $平行,Ⅱ区域宽度为$ d $。质量为$ m $、电荷量为$ + q $的粒子可在边界$ AD $上的不同点射入,入射速度垂直$ AD $且垂直磁场,若入射速度大小为$ \frac{qBd}{m} $,不计粒子重力,则

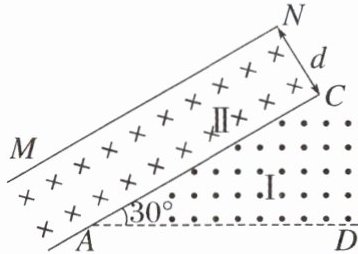
A.粒子在磁场中运动的半径为$ \frac{d}{2} $
B.粒子在距$ A $点$ 0.5d $处射入,不会进入Ⅱ区域
C.粒子在距$ A $点$ 1.5d $处射入,在Ⅰ区域内运动的时间为$ \frac{\pi m}{qB} $
D.能够进入Ⅱ区域的粒子,在Ⅱ区域内运动的最短时间为$ \frac{\pi m}{3qB} $

答案：
6.CD [带电粒子在磁场中的运动半径$r=\frac{mv}{qB}=d$，选项A错误;设从某处$E$进入磁场的粒子，其轨迹恰好与$AC$相切(如图所示)，则$E$点与$A$点的距离为$AO - EO=2d - d = d$，粒子在距$A$点$0.5d$处射入，会进入Ⅱ区域，选项B错误;粒子在距$A$点$1.5d$处射入，不会进入Ⅱ区域，在Ⅰ区域内的轨迹为半圆，运动的时间为$t=\frac{T}{2}=\frac{\pi m}{qB}$，选项C正确;进入Ⅱ区域的粒子，弦长最短时的运动时间最短，且最短弦长为$d$，与半径相同，故对应圆心角为$60^{\circ}$，最短时间为$t_{\min}=\frac{T}{6}=\frac{\pi m}{3qB}$，选项D正确。]

7. (14分)(2024·丽水市高二期中)如图所示,在$ x $轴上方存在垂直于$ xOy $平面向外的匀强磁场,坐标原点$ O $处有一粒子源,可向$ x $轴和$ x $轴上方的$ xOy $平面各个方向不断地发射质量为$ m $、带电量为$ + q $、速度大小均为$ v $的粒子。在$ x $轴上距离原点$ x_{0} $处垂直于$ x $轴放置一个长度为$ x_{0} $、厚度不计、两侧均能接收粒子的薄金属板$ P $(粒子打在金属板$ P $上即被吸收,电势保持为0)。沿$ y $轴正方向射出的粒子恰好打在薄金属板的上端,不计带电粒子的重力和粒子间相互作用力。
(1)(4分)求磁感应强度$ B $的大小;
(2)(6分)求被薄金属板接收的粒子在磁场运动的最短时间与最长时间;
(3)(4分)要使薄金属板$ P $右侧不能接收到粒子,求挡板沿$ x $轴正方向移动的最小距离。

答案：
7.
(1)$\frac{mv}{qx_{0}}$
(2)$\frac{\pi x_{0}}{3v}$ $\frac{5\pi x_{0}}{3v}$
$(\sqrt{3}-1)x_{0}$
解析
(1)设粒子做圆周运动的半径为$R$，由几何关系，得$R = x_{0}$，
根据牛顿第二定律，得$qvB=\frac{mv^{2}}{R}$，
联立解得$B=\frac{mv}{qx_{0}}$。
(2)带电粒子在磁场中的运动周期为$T$，
则有$T=\frac{2\pi R}{v}$，
得$T=\frac{2\pi x_{0}}{v}$，
打在$P$左侧下端的粒子在磁场中运动的时间最短，如图。
由几何关系可知，打在$P$左侧下端的粒子在磁场中偏转的角度是$\theta_{1}=60^{\circ}$，
运动的最短时间$t_{\min}=\frac{\theta_{1}}{360^{\circ}}T$，
联立解得$t_{\min}=\frac{\pi x_{0}}{3v}$。
打在$P$右侧下端的粒子在磁场中运动的时间最长，
如图。
由几何关系可知，打在$P$右侧下端的粒子在磁场中偏转的角度是$\theta_{2}=300^{\circ}$，
运动的最长时间$t_{\max}=\frac{\theta_{2}}{360^{\circ}}T$，
联立解得$t_{\max}=\frac{5\pi x_{0}}{3v}$。
(3)要使挡板右侧无粒子到达，$P$板最上端与$O$点的连线长应为$2x_{0}$，
即粒子圆周运动的直径，如图所示。
所以沿$x$轴正方向移动的最小长度为$\Delta x=ON - OM=\sqrt{(2x_{0})^{2}-x_{0}^{2}}-x_{0}=(\sqrt{3}-1)x_{0}$。