《2025年步步高精准讲练物理选择性必修第二册》

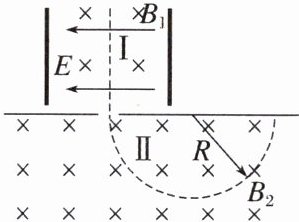
1. (2024·杭州十四中学高二期中)如图有一混合正离子束先后通过正交电场磁场区域Ⅰ和匀强磁场区域Ⅱ,如果这束正离子束流在区域Ⅰ中不偏转,进入区域Ⅱ后偏转半径又相同,则说明这些正离子具有相同的


A.动能
B.质量
C.电荷
D.荷质比

答案： 1.D [这束正离子束流在区域Ⅰ中不偏转，则有 $qE = qvB_1$，可得 $v = \frac{E}{B_1}$，进入区域Ⅱ后偏转半径又相同，由洛伦兹力提供向心力有 $qvB_2 = m\frac{v^2}{r}$，可得 $r = \frac{mv}{qB_2} = \frac{mE}{qB_1B_2}$，可知这些正离子具有相同的速度和荷质比，故选 D。]

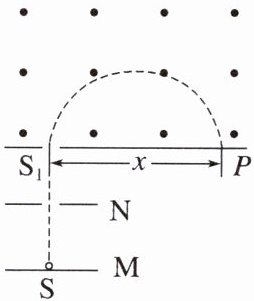
2. (多选)(2024·杭州市高二期末)质谱仪是一种测定带电粒子质量或分析同位素的重要设备,它的构造原理如图所示,离子源 S 产生比荷为 k 的离子束(速度可视为零),经 M、N 两板间大小为 U 的加速电压加速后从小孔 S₁ 垂直于磁感线进入匀强磁场,运转半周后到达照相底片上的 P 点。已知 P 点到小孔 S₁ 的距离为 x,匀强磁场的方向垂直纸面向外,则下列说法不正确的是


A.N 板带正电
B.离子进入匀强磁场的速度大小为$\sqrt{2kU}$
C.匀强磁场的磁感应强度大小为$\frac{2}{x}\sqrt{\frac{2U}{k}}$
D.x 相同,对应离子的比荷可能不相等

答案： 2.AD [由左手定则结合离子在磁场中偏转方向可知离子带正电，所以加速电场的 N 板带负电，故 A 错误，与题意相符；由动能定理，可得 $qU = \frac{1}{2}mv^2$，又 $\frac{q}{m} = k$，联立解得 $v = \sqrt{2kU}$，故 B 正确，与题意不符；带电离子在磁场中做匀速圆周运动，有 $qvB = m\frac{v^2}{r}$，由几何关系，可得 $x = 2r$，联立解得 $B = \frac{2}{x}\sqrt{\frac{2U}{k}}$ 由此可知 $x$ 相同，磁感应强度 $B$ 相同，则对应离子的比荷相等，故 C 正确，与题意不符，D 错误，与题意相符。]

3. 回旋加速器的原理如图所示,下列说法正确的是

A.两个 D 形盒之间的窄缝区域存在恒定的电场
B.带电粒子经过 D 形盒区域时被加速
C.D 形盒区域既存在磁场又存在电场
D.带电粒子不断被加速,每运动半圈所用的时间却保持不变

答案： 3.D [两个 D 形盒之间的窄缝区域存在交变电场，D 形盒区域只存在磁场。静电力对粒子做正功，使粒子加速，磁场力对粒子不做功，不改变速度的大小，只改变速度的方向，粒子在磁场中的回旋周期与速率无关，因此每运动半圈所用的时间保持不变，故选 D。]

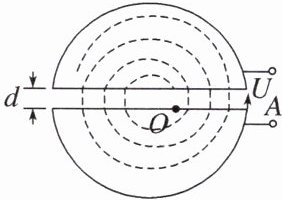
4. (多选)(2024·宁波市高二期中)CT 是医院常用的一种仪器,CT 的重要部件之一就是粒子回旋加速器,回旋加速器的结构如图所示,有一磁感应强度为 B 的匀强磁场垂直于回旋加速器。在 CT 回旋加速器的 O 点可以释放初速度为零、质量为 m、电荷量为 q 的粒子(不计粒子重力)。粒子经过加速、回旋,最后从 A 点射出并获得最大动能 $E_k$,两 D 形盒之间的距离为 d、加速电压为 U,则下列说法正确的是


A.D 形盒的最大半径为$\frac{\sqrt{2mE_k}}{qB}$
B.粒子在加速器中运动的圈数为$\frac{E_k}{qU}$
C.回旋加速器所加交流电压的频率为$\frac{2\pi m}{qB}$
D.减小加速电压,粒子从加速器射出时的动能不变

答案： 4.AD [粒子获得的最大动能为 $E_k = \frac{1}{2}mv_m^2$，根据洛伦兹力提供向心力 $qv_mB = m\frac{v_m^2}{R_m}$，D 形盒的最大半径为 $R_m = \frac{\sqrt{2mE_k}}{qB}$，故 A 正确；粒子在加速器中运动的圈数为 $n$，粒子每转动一圈被加速两次，有 $E_k = 2nqU$ 粒子在加速器中运动的圈数为 $n = \frac{E_k}{2qU}$，故 B 错误；粒子在磁场中运动的周期为 $T = \frac{2\pi m}{qB}$，回旋加速器所加交流电压的频率为 $f = \frac{1}{T} = \frac{qB}{2\pi m}$，故 C 错误；根据洛伦兹力提供向心力 $qvB = m\frac{v^2}{R}$，粒子从加速器射出时的动能为 $E_k' = \frac{1}{2}mv^2 = \frac{q^2B^2R^2}{2m}$，减小加速电压，D 形盒的最大半径不变，粒子从加速器射出的动能不变，故 D 正确。]

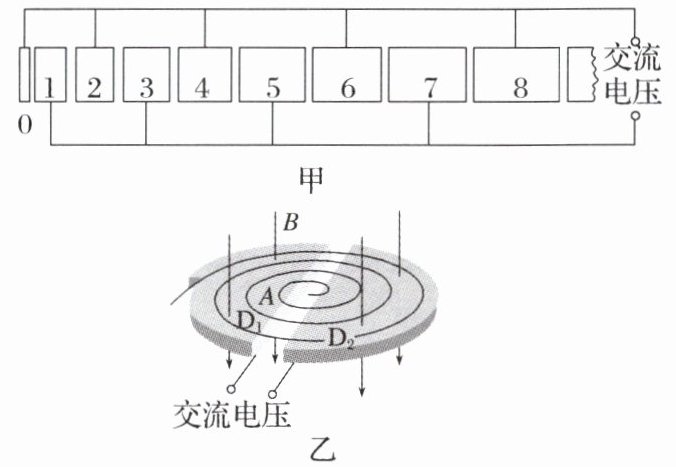
5. (2024·舟山市高二期末)如图所示,图甲为直线加速器,它由多个横截面积相同的金属圆筒共轴依次排列,圆筒长度按照一定的规律依次增加。被加速的带电粒子在金属圆板 0 中心处由静止释放,之后每次通过圆筒间隙都被加速,且加速时间可以忽略不计。图乙为回旋加速器,D₁、D₂为两个中空的半圆形金属盒,处于竖直向下的匀强磁场 B 中。被加速的带电粒子在 A 点由静止释放,之后每次通过 D 形盒间隙都会被加速,且加速时间也可以忽略不计。在粒子运动的过
[图甲为直线加速器，图乙为回旋加速器]

A.带电粒子在直线加速器的金属圆筒中做匀速直线运动
B.直线加速器中,1、2、3 金属圆筒长度之比为 1:2:3
C.若用回旋加速器加速不同种类的粒子,则必须改变其所接交流电源的频率
D.带电粒子通过回旋加速器后获得的最大速度与加速电压有关

答案： 5.A [直线加速器中的金属圆筒起到了静电屏蔽的作用，其内部电场强度为零，因此带电粒子在圆筒中做匀速直线运动，故 A 正确；直线加速器中，带电粒子在金属圆板 O 中心处由静止释放，由于每两个金属筒之间的电压交替变化，粒子每次经过金属筒间时都要被加速，可知粒子经过每个金属筒的时间一定相同（为交流电的半个周期，即 $\frac{T}{2}$)，设金属筒间的电压为 $U$，粒子的电荷量为 $q$，质量为 $m$，则粒子第一次被加速后由动能定理有 $qU = \frac{1}{2}mv_1^2$，粒子在金属筒中做匀速直线运动，可得第一个金属筒的长度为 $L_1 = v_1 · \frac{T}{2}$，粒子第二次被加速由动能定理有 $2qU = \frac{1}{2}mv_2^2$，可得第二个金属筒的长度为 $L_2 = v_2 · \frac{T}{2}$，粒子第三次被加速由动能定理有 $3qU = \frac{1}{2}mv_3^2$，可得第三个金属筒的长度为 $L_3 = v_3 · \frac{T}{2}$，联立可得 $L_1 : L_2 : L_3 = 1 : \sqrt{2} : \sqrt{3}$，故 B 错误；回旋加速器所接交流电源的频率为 $f = \frac{1}{T} = \frac{1}{2\pi m} = \frac{qB}{2\pi m}$，可知若不同种类的粒子的荷质比相同，不需要改变其所接交流电源的频率，故 C 错误；在回旋加速器的磁场中，当粒子的运动半径等于 D 形盒的半径 $R$ 时，粒子获得的速度最大，根据洛伦兹力提供向心力有 $qv_mB = m\frac{v_m^2}{R}$，可得 $v_m = \frac{qBR}{m}$，故带电粒子通过回旋加速器后获得的最大速度与加速电压无关，故 D 错误。]