《2025年新课程课堂同步练习册八年级数学上册人教版》

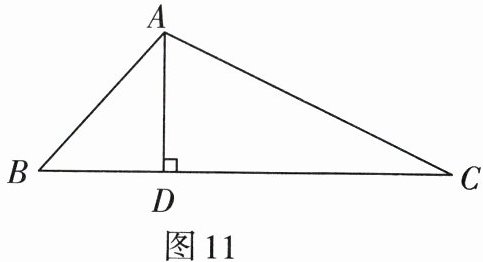
5. 如图11,在$\triangle ABC$中,$\angle BAC= 120^{\circ}$,$AD\bot BC$于D,$AB+BD= DC$,求$\angle C$的大小.

答案： 20°. 提示:在 DC 上取 DE,使得 DE=DB,连接 AE,可得 EA=EC.

6. 如图12,在四边形ABCD中,$AB= AD$,$CB= CD$,$\angle A= 60^{\circ}$,点E为AD上一点,连接BD,CE交于点F,$CE// AB$.
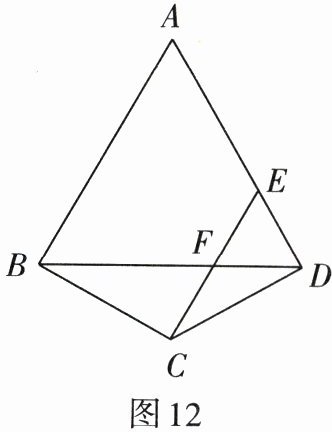
(1)判断$\triangle DEF$的形状,并说明理由；
(2)若$AD= 12$,$CE= 8$,求CF的长.

答案：
(1)提示:△DEF 是等边三角形. 证△ABD 是等边三角形. 再由 CE//AB,得∠CED=∠A=60°,∠DFE=∠ABD=60°,
∴∠CED=∠ADB=∠DFE,
∴△DEF 是等边三角形.
(2)提示:连接 AC 交 BD 于点 O,证 AC 是 BD 的垂直平分线,即 AC⊥BD. 再证 AE=CE=8,
∴DE=AD-AE=12-8=4.
∵△DEF 是等边三角形,
∴EF=DE=4,
∴CF=CE-EF=8-4=4.