《2025年阳光课堂金牌练习册八年级数学上册人教版》

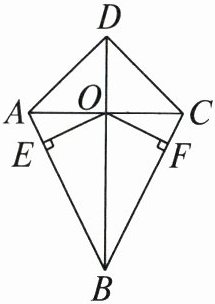
18. 如图,在四边形$ABCD$中,$AC与BD相交于点O$,$OE\perp AB于点E$,$OF\perp BC于点F$,$BD平分\angle ABC$,$AB = CB$.求证$\triangle OAD\cong\triangle OCD$.

答案： 证明：
1.
∵BD平分∠ABC（已知），
∴∠ABD=∠CBD（角平分线定义）。
2. 在△ABD和△CBD中，
$\left\{\begin{array}{l} AB=CB\ (已知) \\ ∠ABD=∠CBD\ (已证) \\ BD=BD\ (公共边) \end{array}\right.$

∴△ABD≌△CBD（SAS）。
3.
∴AD=CD，∠ADB=∠CDB（全等三角形对应边相等、对应角相等）。
4. 在△OAD和△OCD中，
$\left\{\begin{array}{l} AD=CD\ (已证) \\ ∠ADO=∠CDO\ (已证,∠ADB=∠CDB) \\ OD=OD\ (公共边) \end{array}\right.$

∴△OAD≌△OCD（SAS）。

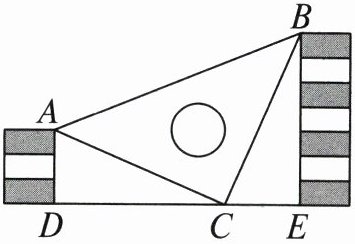
19. 如图,小林用$10块高度是3\mathrm{cm}的长方体木条垒了2$个与地面垂直的木块,两个木块之间刚好放进一个等腰直角三角尺,其中$\angle ACB = 90^{\circ}$,点$C在DE$上,点$A$,$B$与两个木块的顶端重合.求两个木块之间的距离.

答案： 解：设两个木块的高度分别为$AD$和$BE$，每块木条高度为$3\,cm$，设左边木块用$a$块木条，右边用$b$块木条，则$a + b=10$，故$AD = 3a\,cm$，$BE=3b\,cm$。
因为木块与地面垂直，所以$AD\perp DE$，$BE\perp DE$，即$\angle ADC=\angle BEC = 90°$。
$\triangle ACB$为等腰直角三角形，$\angle ACB=90°$，则$AC = BC$，$\angle ACD+\angle BCE=90°$。
在$Rt\triangle ADC$中，$\angle ACD+\angle CAD=90°$，故$\angle CAD=\angle BCE$。
同理，$\angle ACD=\angle CBE$。
在$\triangle ADC$和$\triangle CEB$中，$\begin{cases}\angle ADC=\angle CEB\\\angle CAD=\angle BCE\\AC = CB\end{cases}$，所以$\triangle ADC\cong\triangle CEB(AAS)$。
因此$AD = CE$，$DC=BE$。
两个木块之间的距离$DE=DC + CE=BE + AD=3b + 3a=3(a + b)=3×10 = 30\,cm$。
答：两个木块之间的距离为$30\,cm$。

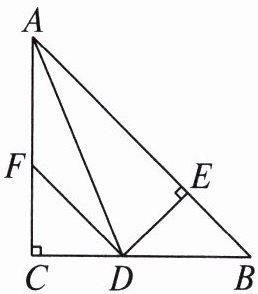
20. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AD是\angle BAC$的平分线,$DE\perp AB交AB于点E$,点$F在AC$上,$BD = DF$.求证：
(1)$CD = ED$；
(2)$AB = AF + 2EB$.

答案：
(1)证明：
∵AD是∠BAC的平分线，∠C=90°，DE⊥AB，
∴CD=ED（角平分线上的点到角两边的距离相等）。
(2)证明：在△ACD和△AED中，
∠CAD=∠EAD（AD是角平分线），
∠C=∠AED=90°，
AD=AD，
∴△ACD≌△AED(AAS)，
∴AC=AE。
在Rt△DFC和Rt△DBE中，
DF=BD（已知），
CD=ED（已证），
∴Rt△DFC≌Rt△DBE(HL)，
∴FC=EB。
∵AC=AF+FC，
∴AE=AF+EB。
∵AB=AE+EB，
∴AB=AF+EB+EB=AF+2EB。