《2025年阳光课堂金牌练习册八年级数学上册人教版》

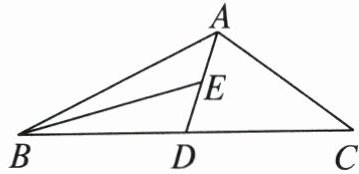
19. 如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE= 15°,∠BAD= 35°,求∠BED的度数；
(2)在△BED中作BD边上的高；
(3)若△ABC的面积为60,BD= 5,求点E到BC边的距离.

答案：
(1)
在$\triangle ABD$中，已知$\angle ABE = 15^{\circ}$，$\angle BAD = 35^{\circ}$。
根据三角形外角性质，$\angle BED=\angle ABE + \angle BAD$，所以$\angle BED = 15^{\circ}+35^{\circ}=50^{\circ}$。
(2)
过点$E$作$EF\perp BD$于点$F$，则$EF$为$\triangle BED$中$BD$边上的高。
(3)
因为$AD$为$\triangle ABC$的中线，所以$S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}$。
已知$S_{\triangle ABC}=60$，则$S_{\triangle ABD}=\frac{1}{2}×60 = 30$。
因为$BE$为$\triangle ABD$的中线，所以$S_{\triangle BED}=\frac{1}{2}S_{\triangle ABD}$，则$S_{\triangle BED}=\frac{1}{2}×30 = 15$。
已知$BD = 5$，设点$E$到$BD$边的距离为$h$，根据三角形面积公式$S=\frac{1}{2}×底×高$，可得$\frac{1}{2}× BD× h = 15$，即$\frac{1}{2}×5× h = 15$，解得$h = 6$，所以点$E$到$BC$边（因为$E$到$BD$距离与$E$到$BC$距离在此题情境下等价，$BD$在$BC$上）的距离为$6$。
综上，答案依次为：
(1)$50^{\circ}$；
(2)过点$E$作$EF\perp BD$于点$F$；
(3)$6$。

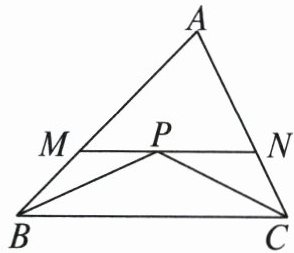
20. 如图,已知P为△ABC内部一点,连接BP,PC. 过点P作直线交AB,AC于点M,N,证明：AB+AC＞PB+PC.

答案： 在△BMP中，由三角形三边关系得：BM + MP ＞ BP。
在△CNP中，由三角形三边关系得：CN + NP ＞ CP。
两式相加：BM + MP + CN + NP ＞ BP + CP，即BM + CN + MN ＞ BP + CP。
在△AMN中，由三角形三边关系得：AM + AN ＞ MN。
两边同时加BM + CN：AM + AN + BM + CN ＞ BM + CN + MN。
又
∵AB = AM + BM，AC = AN + CN，
∴AB + AC ＞ BM + CN + MN。
综上，AB + AC ＞ BM + CN + MN ＞ BP + CP，即AB + AC ＞ PB + PC。
结论：AB + AC＞PB+PC。

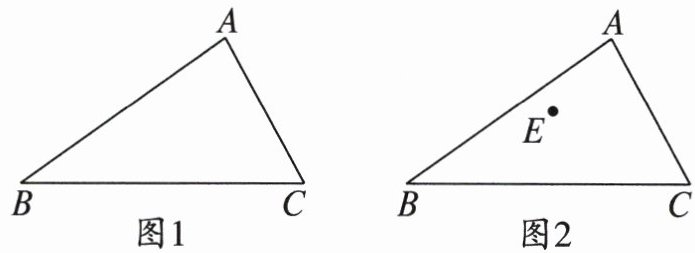
21. 如图1,有一块三角形菜地,若从顶点A修一条笔直的小路交BC于点D,小路正好将菜地分成面积相等的两部分.
(1)画出点D的位置.
(2)假设在菜地中有一点E,如图2,BC上是否存在点F,使折线A-E-F将△ABC分为面积相等的两部分？若存在,请画出点F的位置,并说明理由.

答案：
(1) 作BC的中点D，连接AD，点D即为所求。
(2) 存在点F。
作法：①连接AE；②取BC的中点D；③过点D作DF//AE交BC于点F。点F即为所求。
理由：
∵D为BC中点，
∴AD为△ABC中线，S△ABD=1/2S△ABC。
∵DF//AE，
∴S△AEF=S△AED（同底等高），
∴折线A-E-F所分区域面积等于1/2S△ABC。