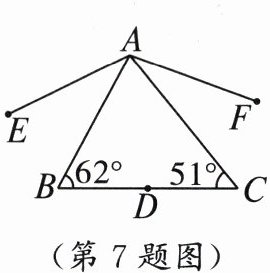
7. 如图,在△ABC 中,点 D 在 BC 上,将点 D 分别以 AB,AC 为对称轴,画出对称点 E,F,并连接 AE,AF,则∠EAF 为(
A.134°
B.129°
C.124°
D.113°
A
)
A.134°
B.129°
C.124°
D.113°
答案:
A
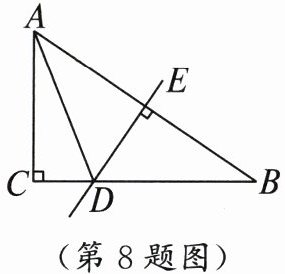
8. (2024·四川凉山州中考)如图,在 Rt△ABC 中,∠ACB = 90°,DE 垂直平分 AB 交 BC 于点 D,连接 AD,若△ACD 的周长为 50 cm,则 AC + BC = (
A.25 cm
B.45 cm
C.50 cm
D.55 cm
C
)
A.25 cm
B.45 cm
C.50 cm
D.55 cm
答案:
C
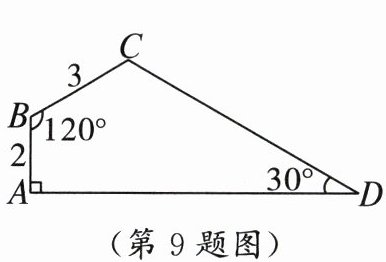
9. 如图,在四边形 ABCD 中,∠A = 90°,∠B = 120°,∠D = 30°,AB = 2,BC = 3,则 CD = (
A.5
B.6
C.7
D.8
C
)
A.5
B.6
C.7
D.8
答案:
C
10. 已知点 P 是等边三角形 ABC 的边 BC 上的一点,若∠APC = 104°,则在线段 AP,BP,CP 为边的三角形中,最小内角的大小为(
A.14°
B.16°
C.24°
D.26°
B
)A.14°
B.16°
C.24°
D.26°
答案:
B
11. 已知点 A 关于 x 轴的对称点为 B(m,3),关于 y 轴的对称点为 C(2,n),那么 m + n =
-5
。
答案:
-5
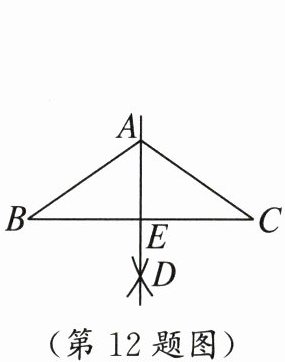
12. 如图,在△ABC 中,AB = AC。分别以点 B 和点 C 为圆心,大于 $\frac{1}{2}$BC 的长为半径作弧,两弧交于点 D,作直线 AD 交 BC 于点 E。若∠BAC = 110°,则∠BAE 为
55°
。
答案:
55°
13. (2024·甘肃中考)围棋起源于中国,古代称为“弈”。两位同学的部分对弈图如图所示,轮到白方落子,观察棋盘,白方如果落子于点
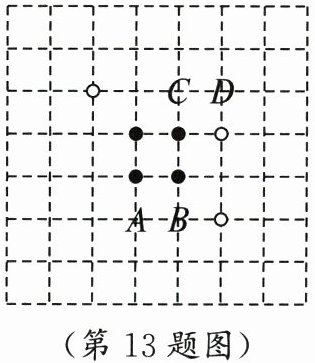
A
的位置,则所得的对弈图是轴对称图形。(填写 A,B,C,D 中的一处即可,A,B,C,D 位于棋盘的格点上)
答案:
A
14. 如图,△ABC 是等边三角形,点 D 是 BC 边上任意一点,DE ⊥ AB 于点 E,DF ⊥ AC 于点 F。若 BC = 4,则 BE + CF =
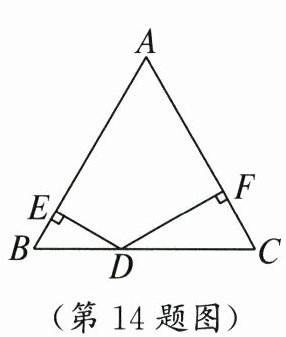
2
。
答案:
2
15. 如图,已知∠AOB = 50°,点 P 为∠AOB 内部一点,点 M,N 分别为射线 OA,OB 上的两个动点,当△PMN 的周长最小时,∠MPN =
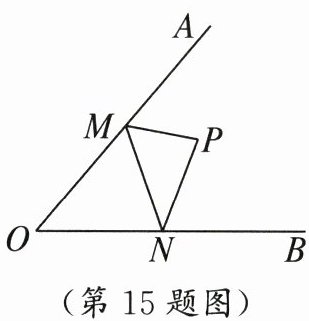
80°
。
答案:
80°
查看更多完整答案,请扫码查看


