11. (2024·重庆中考)计算:$\vert - 2\vert+3^{0}= $
3
。
答案:
3
12. $(-x^{3})^{2}-x^{4}(2x^{2}-x + 1)= $
$-x^{6} + x^{5} - x^{4}$
。
答案:
$-x^{6} + x^{5} - x^{4}$(或写为:$- x ^ { 6 } + x ^ { 5 } - x ^ { 4 }$)。
13. 现新定义一种运算:$a※b= (-3)^{a}\cdot3^{b}÷9^{a - b}$,则$5※3= $
$-81$
。
答案:
$-81$
14. 按图中所示的方式分割正方形,可得到的结论为:$(x + y)^{2}-$
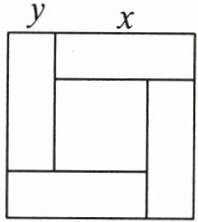
$(x - y)^2$
$=4xy$。
答案:
$(x - y)^2$
15. 观察下列单项式:$a$,$-3a^{2}$,$9a^{3}$,$-27a^{4}$,$81a^{5}$,…,从第二个单项式开始,计算每个单项式与它前一个单项式的商,你发现的规律是
每个商都是$-3a$
,按照这一规律,第七个单项式应是$729a^{7}$
。
答案:
每个商都是$-3a$;$729a^{7}$
16. 已知实数a,b满足$a + b= 2,ab= \frac{3}{4},$则a - b的值为
±1
。
答案:
±1
17. 计算:(1)$2x\cdot x^{3}+(x^{2})^{2}$;(2)$(a^{2}b)^{4}÷(-a^{2}b)^{3}$。
答案:
(1)
首先,根据同底数幂的乘法法则,计算 $2x\cdot x^{3}$:
$2x\cdot x^{3} = 2x^{1+3} = 2x^{4}$
接着,根据幂的乘方法则,计算 $(x^{2})^{2}$:
$(x^{2})^{2} = x^{2 × 2} = x^{4}$
最后,将两部分相加:
$2x^{4} + x^{4} = 3x^{4}$
(2)
首先,根据积的乘方法则,计算 $(a^{2}b)^{4}$:
$(a^{2}b)^{4} = a^{2 × 4}b^{4} = a^{8}b^{4}$
接着,计算 $(-a^{2}b)^{3}$:
$(-a^{2}b)^{3} = (-1)^{3}a^{2 × 3}b^{3} = -a^{6}b^{3}$
最后,根据同底数幂的除法法则,进行除法运算:
$\frac{a^{8}b^{4}}{-a^{6}b^{3}} = \frac{a^{8}}{a^{6}} × \frac{b^{4}}{b^{3}} × \frac{1}{-1} = a^{8-6}b^{4-3} × (-1) = -a^{2}b$
(1)
首先,根据同底数幂的乘法法则,计算 $2x\cdot x^{3}$:
$2x\cdot x^{3} = 2x^{1+3} = 2x^{4}$
接着,根据幂的乘方法则,计算 $(x^{2})^{2}$:
$(x^{2})^{2} = x^{2 × 2} = x^{4}$
最后,将两部分相加:
$2x^{4} + x^{4} = 3x^{4}$
(2)
首先,根据积的乘方法则,计算 $(a^{2}b)^{4}$:
$(a^{2}b)^{4} = a^{2 × 4}b^{4} = a^{8}b^{4}$
接着,计算 $(-a^{2}b)^{3}$:
$(-a^{2}b)^{3} = (-1)^{3}a^{2 × 3}b^{3} = -a^{6}b^{3}$
最后,根据同底数幂的除法法则,进行除法运算:
$\frac{a^{8}b^{4}}{-a^{6}b^{3}} = \frac{a^{8}}{a^{6}} × \frac{b^{4}}{b^{3}} × \frac{1}{-1} = a^{8-6}b^{4-3} × (-1) = -a^{2}b$
18. 用简便方法计算:
(1)$202×198 + 4$;(2)$501^{2}$。
(1)$202×198 + 4$;(2)$501^{2}$。
答案:
(1) 原式=(200+2)(200-2)+4
=200²-2²+4
=40000-4+4
=40000
(2) 原式=(500+1)²
=500²+2×500×1+1²
=250000+1000+1
=251001
(1) 原式=(200+2)(200-2)+4
=200²-2²+4
=40000-4+4
=40000
(2) 原式=(500+1)²
=500²+2×500×1+1²
=250000+1000+1
=251001
查看更多完整答案,请扫码查看


