《2025年阳光课堂金牌练习册八年级数学上册人教版》

19. 如图,在 Rt△ABC 中,∠ACB = 90°,D 是 BC 延长线上的一点,BD 的垂直平分线交 AB 于点 E,DE 交 AC 于点 F。求证：点 E 在线段 AF 的垂直平分线上。

答案： 证明：设BD的垂直平分线与BD交于点M，则EM⊥BD，且ED=EB（垂直平分线性质）。
∵ED=EB，
∴∠EDB=∠B（等边对等角）。
∵∠ACB=90°，D在BC延长线上，
∴AC⊥BD。又EM⊥BD，
∴AC//EM（垂直于同一直线的两直线平行）。
∴∠A=∠BEM（两直线平行，同位角相等）。
在Rt△EMB中，∠EMB=90°，
∴∠BEM+∠B=90°。
在Rt△ABC中，∠ACB=90°，
∴∠A+∠B=90°。
∴∠A=∠BEM（等量代换）。
在Rt△DCF中，∠DCF=90°，
∴∠EDB+∠DFC=90°。
∵∠DFC=∠AFE（对顶角相等），∠EDB=∠B，
∴∠B+∠AFE=90°。
又∠A+∠B=90°，
∴∠A=∠AFE（同角的余角相等）。
∴EA=EF（等角对等边）。
∴点E在线段AF的垂直平分线上（到线段两端距离相等的点在垂直平分线上）。

20. 如图,在△ABC 中,AB = AC,D,E 是△ABC 内的两点,AD 平分∠BAC,∠EBC = ∠E = 60°。若 BE = 6 cm,DE = 2 cm,求 BC 的长。

答案： 16cm

21. 在边长为 9 的等边三角形 ABC 中,点 P 是 AB 上一动点,以每秒 1 个单位长度的速度从点 A 向点 B 运动,设运动时间为 t 秒。
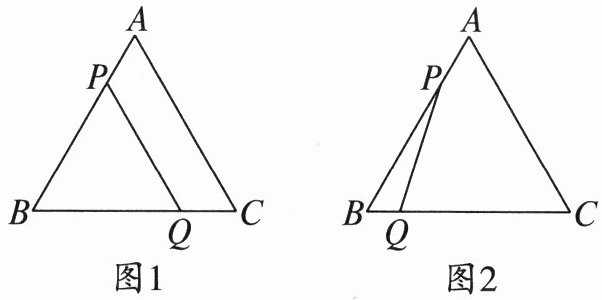
(1) 如图 1,若点 Q 是 BC 上一定点,BQ = 6,PQ // AC,求 t 的值；
(2) 如图 2,若点 P 从点 A 向点 B 运动,同时点 Q 以每秒 2 个单位长度的速度从点 B 经点 C 向点 A 运动,当 t 为何值时,△APQ 为等边三角形？

答案：
(1)
∵△ABC是等边三角形，
∴∠B=60°，AB=BC=9。
∵PQ//AC，
∴△BPQ∽△BAC，
∴$\frac{BP}{BA}=\frac{BQ}{BC}$。
∵AP=t，
∴BP=AB-AP=9-t，BQ=6，
∴$\frac{9-t}{9}=\frac{6}{9}$，解得$9-t=6$，
∴t=3。
(2) 由题意，AP=t（0≤t≤9），Q的运动路程为2t。
当Q在BC上（0≤t≤4.5）时，BQ=2t，CQ=9-2t，此时AQ²=AC²+CQ²-2·AC·CQ·cos60°=9²+(9-2t)²-2×9×(9-2t)×$\frac{1}{2}$，令AQ=AP=t，方程无解。
当Q在CA上（4.5＜t≤9）时，Q运动路程为2t，CA上路程为2t-9，
∴AQ=AC-(2t-9)=18-2t。
∵△APQ为等边三角形，∠PAQ=60°，
∴AP=AQ，即t=18-2t，解得t=6。
(1) t=3；
(2) t=6。