21. (15分)如图,隧道的截面由抛物线和长方形构成,长方形的长是 $ 12 m $,宽是 $ 4 m $。按照图中所示的直角坐标系,抛物线可以用 $ y = -\frac{1}{6}x^2 + bx + c $ 表示,且抛物线上的点 $ C $ 到墙面 $ OB $ 的水平距离为 $ 3 m $,到地面 $ OA $ 的距离为 $ \frac{17}{2} m $。
(1)求该抛物线的函数关系式,并计算出拱顶 $ D $ 到地面 $ OA $ 的距离;
(2)一辆货运汽车载一长方体集装箱后高为 $ 6 m $,宽为 $ 4 m $,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过 $ 8 m $,那么两排灯的水平距离最小是多少米?

(1)求该抛物线的函数关系式,并计算出拱顶 $ D $ 到地面 $ OA $ 的距离;
(2)一辆货运汽车载一长方体集装箱后高为 $ 6 m $,宽为 $ 4 m $,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过 $ 8 m $,那么两排灯的水平距离最小是多少米?

答案:
解:
(1)根据题意得B(0,4),C(3,$\frac{17}{2}$),把B(0,4),C(3,$\frac{17}{2}$)代入y = −$\frac{1}{6}$x² + bx + c 得{c = 4,-$\frac{1}{6}$×3² + 3b + c = $\frac{17}{2}$},解得{b = 2,c = 4}.所以抛物线解析式为y = −$\frac{1}{6}$x² + 2x + 4,则y = −$\frac{1}{6}$(x − 6)² + 10,所以D(6,10),所以拱顶D到地面OA的距离为10m.
(2)由题意得货运汽车最外侧与地面OA 的交点为(2,0)或(10,0),当x = 2或x = 10时,y = $\frac{22}{3}$>6,所以这辆货车能安全通过.
(3)令y = 8,则−$\frac{1}{6}$(x − 6)² + 10 = 8,解得x₁ = 6 + 2$\sqrt{3}$,x₂ = 6 − 2$\sqrt{3}$,则x₁ - x₂ = 4$\sqrt{3}$,所以两排灯的水平距离最小是4$\sqrt{3}$m.
(1)根据题意得B(0,4),C(3,$\frac{17}{2}$),把B(0,4),C(3,$\frac{17}{2}$)代入y = −$\frac{1}{6}$x² + bx + c 得{c = 4,-$\frac{1}{6}$×3² + 3b + c = $\frac{17}{2}$},解得{b = 2,c = 4}.所以抛物线解析式为y = −$\frac{1}{6}$x² + 2x + 4,则y = −$\frac{1}{6}$(x − 6)² + 10,所以D(6,10),所以拱顶D到地面OA的距离为10m.
(2)由题意得货运汽车最外侧与地面OA 的交点为(2,0)或(10,0),当x = 2或x = 10时,y = $\frac{22}{3}$>6,所以这辆货车能安全通过.
(3)令y = 8,则−$\frac{1}{6}$(x − 6)² + 10 = 8,解得x₁ = 6 + 2$\sqrt{3}$,x₂ = 6 − 2$\sqrt{3}$,则x₁ - x₂ = 4$\sqrt{3}$,所以两排灯的水平距离最小是4$\sqrt{3}$m.
22. (16分)在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形 $ ABCD $ 与边长为 $ 2\sqrt{2} $ 的正方形 $ AEFG $ 按图①的位置放置,$ AD $ 与 $ AE $ 在同一直线上,$ AB $ 与 $ AG $ 在同一直线上。
(1)小明发现 $ DG \perp BE $,请你帮他说明理由;
(2)如图②,小明将正方形 $ ABCD $ 绕点 $ A $ 逆时针旋转,当点 $ B $ 恰好落在线段 $ DG $ 上时,请你帮他求出此时 $ BE $ 的长;
(3)如图③,小明将正方形 $ ABCD $ 绕点 $ A $ 继续逆时针旋转,线段 $ DG $ 与线段 $ BE $ 相交,交点为 $ H $,写出 $ \triangle GHE $ 与 $ \triangle BHD $ 面积之和的最大值,并简要说明理由。

(1)小明发现 $ DG \perp BE $,请你帮他说明理由;
(2)如图②,小明将正方形 $ ABCD $ 绕点 $ A $ 逆时针旋转,当点 $ B $ 恰好落在线段 $ DG $ 上时,请你帮他求出此时 $ BE $ 的长;
(3)如图③,小明将正方形 $ ABCD $ 绕点 $ A $ 继续逆时针旋转,线段 $ DG $ 与线段 $ BE $ 相交,交点为 $ H $,写出 $ \triangle GHE $ 与 $ \triangle BHD $ 面积之和的最大值,并简要说明理由。

答案:
解:
(1)
∵四边形ABCD和四边形AEFG 都为正方形,
∴AD = AB,∠DAG = ∠BAE = 90°,AG = AE,
∴△ADG ≌ △ABE,
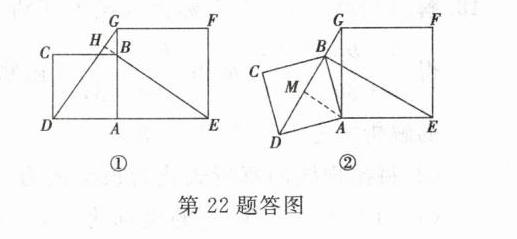
∴∠AGD = ∠AEB.如答图①,延长EB交DG于点H,在△ADG中,∠AGD + ∠ADG = 90°,
∴∠AEB + ∠ADG = 90°,在△EDH中,
∵∠AEB + ∠ADG + ∠DHE = 180°,
∴∠DHE = 90°,
∴DG⊥BE.
(2)
∵四边形ABCD和四边形AEFG都为正方形,
∴AD = AB,∠DAB = ∠GAE = 90°,AG = AE,
∴∠DAB + ∠BAG = ∠GAE + ∠BAG,即∠DAG = ∠BAE.在△ADG和△ABE中,AD = AB,
∵{∠DAG = ∠BAE,AG = AE,
∴△ADG ≌ △ABE,
∴DG = BE.如答图②,过点A作AM⊥DG交DG于点M,则∠AMD = ∠AMG = 90°.
∵BD为正方形ABCD的对角线,
∴∠MDA = 45°.在Rt△AMD中,
∵∠MDA = 45°,∠AMD = 90°,又
∵AD = 2,
∴DM = AM = $\sqrt{2}$.在Rt△AMG中,根据勾股定理得:GM = $\sqrt{AG² - AM²}$ = $\sqrt{6}$,
∵DG = DM + GM = $\sqrt{2}$ + $\sqrt{6}$,
∴BE = DG = $\sqrt{2}$ + $\sqrt{6}$.
(3)△GHE和△BHD面积之和的最大值为6.理由如下:对于△EGH,点H在以EG为直径的圆上,
∴当点H与点A重合时,△EGH的高最大;对于△BDH,点H在以BD为直径的圆上,
∴当点H与点A重合时,△BDH的高最大,则△GHE和△BHD 面积之和的最大值为2 + 4 = 6.
解:
(1)
∵四边形ABCD和四边形AEFG 都为正方形,
∴AD = AB,∠DAG = ∠BAE = 90°,AG = AE,
∴△ADG ≌ △ABE,
∴∠AGD = ∠AEB.如答图①,延长EB交DG于点H,在△ADG中,∠AGD + ∠ADG = 90°,
∴∠AEB + ∠ADG = 90°,在△EDH中,
∵∠AEB + ∠ADG + ∠DHE = 180°,
∴∠DHE = 90°,
∴DG⊥BE.
(2)
∵四边形ABCD和四边形AEFG都为正方形,
∴AD = AB,∠DAB = ∠GAE = 90°,AG = AE,
∴∠DAB + ∠BAG = ∠GAE + ∠BAG,即∠DAG = ∠BAE.在△ADG和△ABE中,AD = AB,
∵{∠DAG = ∠BAE,AG = AE,
∴△ADG ≌ △ABE,
∴DG = BE.如答图②,过点A作AM⊥DG交DG于点M,则∠AMD = ∠AMG = 90°.
∵BD为正方形ABCD的对角线,
∴∠MDA = 45°.在Rt△AMD中,
∵∠MDA = 45°,∠AMD = 90°,又
∵AD = 2,
∴DM = AM = $\sqrt{2}$.在Rt△AMG中,根据勾股定理得:GM = $\sqrt{AG² - AM²}$ = $\sqrt{6}$,
∵DG = DM + GM = $\sqrt{2}$ + $\sqrt{6}$,
∴BE = DG = $\sqrt{2}$ + $\sqrt{6}$.
(3)△GHE和△BHD面积之和的最大值为6.理由如下:对于△EGH,点H在以EG为直径的圆上,
∴当点H与点A重合时,△EGH的高最大;对于△BDH,点H在以BD为直径的圆上,
∴当点H与点A重合时,△BDH的高最大,则△GHE和△BHD 面积之和的最大值为2 + 4 = 6.

查看更多完整答案,请扫码查看


