7. 如图,有一个质地均匀的正四面体,其四个面上分别画着圆、等边三角形、菱形、正五边形,投掷该正四面体一次,向下的一面的图形既是轴对称图形又是中心对称图形的概率是(
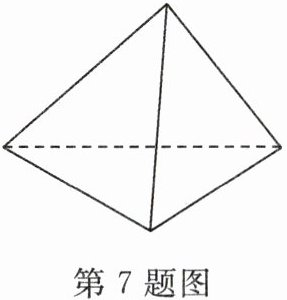
A.1
B.$\frac{1}{4}$
C.$\frac{3}{4}$
D.$\frac{1}{2}$
D
)
A.1
B.$\frac{1}{4}$
C.$\frac{3}{4}$
D.$\frac{1}{2}$
答案:
D
8. 如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是(

A.$\frac{1}{5}$
B.$\frac{2}{5}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
C
)
A.$\frac{1}{5}$
B.$\frac{2}{5}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
答案:
C
9. 小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为(
A.$\frac{1}{6}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$
B
)A.$\frac{1}{6}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$
答案:
B
10. 在一个不透明的盒子里有2个红球和$n$个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到红球的概率是$\frac{1}{5}$,则$n$的值为(
A.3
B.5
C.8
D.10
C
)A.3
B.5
C.8
D.10
答案:
C
11. 在盒子里放有三张分别写有整式$a + 1$,$a + 2$,2的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是( )
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{1}{6}$
D.$\frac{3}{4}$
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{1}{6}$
D.$\frac{3}{4}$
答案:
B 点拨:利用树状图解答此题比较简单,如答图所示,具体结论如下:通过树状图可以知道能组成分式的概率是$\frac{4}{6}=\frac{2}{3}$.
B 点拨:利用树状图解答此题比较简单,如答图所示,具体结论如下:通过树状图可以知道能组成分式的概率是$\frac{4}{6}=\frac{2}{3}$.

12. 如图,$□ ABCD的对角线AC$、$BD相交于点O$,$EF$、$GH过点O$,且点$E$、$H在边AB$上,点$G$、$F在边CD$上,向$□ ABCD$内部投掷飞镖(每次均落在$□ ABCD$内,且落在$□ ABCD$内任何一点的机会均等),则飞镖恰好落在阴影区域的概率为(
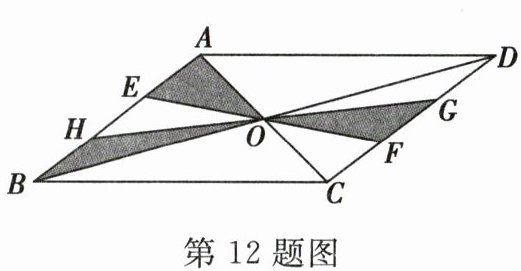
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{8}$
C
)
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{8}$
答案:
C 点拨:
∵四边形$ABCD$为平行四边形,
∴$\triangle OEH$和$\triangle OFG$关于点$O$成中心对称,$\therefore S_{\triangle OEH}=S_{\triangle OFG}$,$\therefore S_{阴影部分}=S_{\triangle AOB}=\frac{1}{4}S_{□ ABCD}$,
∴飞镖恰好落在阴影区域的概率=$\frac{S_{阴影部分}}{S_{□ ABCD}}=\frac{1}{4}$,故选C.
∵四边形$ABCD$为平行四边形,
∴$\triangle OEH$和$\triangle OFG$关于点$O$成中心对称,$\therefore S_{\triangle OEH}=S_{\triangle OFG}$,$\therefore S_{阴影部分}=S_{\triangle AOB}=\frac{1}{4}S_{□ ABCD}$,
∴飞镖恰好落在阴影区域的概率=$\frac{S_{阴影部分}}{S_{□ ABCD}}=\frac{1}{4}$,故选C.
13. 事件$A发生的概率为\frac{1}{20}$,大量重复做这个试验,事件$A$平均每100次发生的次数是
5
.
答案:
5
14. 透明袋子中装有9个球,其中有2个红球、3个绿球和4个蓝球,这些球除颜色外无其他差别. 从袋子中随机取出1个球,则它是红球的概率是
$\frac{2}{9}$
.
答案:
$\frac{2}{9}$
15. 如图,正六边形卡片被分成六个全等的正三角形. 若向该六边形内投掷飞镖,则飞镖落在阴影区域的概率为
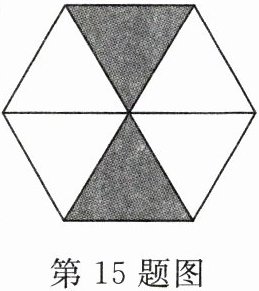
$\frac{1}{3}$
.
答案:
$\frac{1}{3}$
查看更多完整答案,请扫码查看


