《2025年三维数字课堂九年级数学上册人教版》

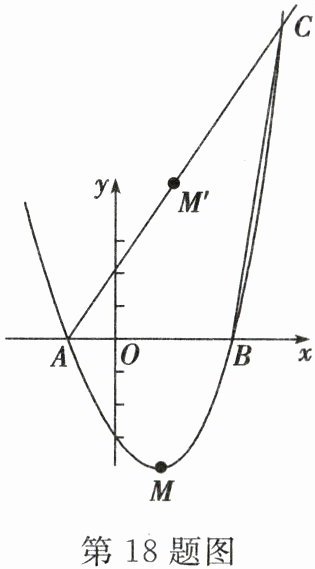
18. (9分)如图,抛物线 $ y = x^2 + bx + c $ 与 $ x $ 轴交于 $ A(-1,0) $,$ B(3,0) $ 两点,顶点 $ M $ 关于 $ x $ 轴的对称点是 $ M' $。
(1)求抛物线的解析式；
(2)若直线 $ AM' $ 与此抛物线的另一个交点为 $ C $,求 $ \triangle CAB $ 的面积。

答案： 解:
(1)将A、B点坐标代入函数解析式，得{1 - b + c = 0,9 + 3b + c = 0}，解得{b = -2,c = -3}，
∴抛物线的解析式为y = x² - 2x - 3.　
(2)将抛物线的解析式化为顶点式为y = (x - 1)² - 4，
∴M点的坐标为(1，−4)，M'点的坐标为(1,4).设AM'的解析式为y = kx + b，将A、M'点的坐标代入，得{-k + b = 0,k + b = 4}，解得{k = 2,b = 2}，
∴AM'的解析式为y = 2x + 2.联立AM'与抛物线，得{y = 2x + 2,y = x² - 2x - 3}，解得{x₁ = -1,y₁ = 0,{x₂ = 5,y₂ = 12}.
∴C点坐标为(5,12)，S△ABC = $\frac{1}{2}$×4×12 = 24.

19. (10分)有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2；乙袋中装有3个完全相同的小球,分别标有数字-1,-2,0。现从甲袋中随机摸取一个小球,记录标有的数字为 $ x $,再从乙袋中随机抽取一个小球,记录标有的数字为 $ y $,确定点 $ M $ 坐标为 $ (x,y) $。
(1)用树状图或列表法列举点 $ M $ 所有可能的坐标；
(2)求点 $ M(x,y) $ 在函数 $ y = -x + 1 $ 的图象上的概率；

答案：
解:
(1)画树状图如答图所示:　

共有9种等可能的结果数，它们是:(0，−1),(0,−2),(0,0),(1,−1),(1,−2),(1,0),(2,−1),(2,−2),(2,0).　
(2)在直线y = −x + 1的图象上的点有(1,0),(2,−1)，所以点M(x,y)在函数y = -x + 1的图象上的概率为$\frac{2}{9}$.

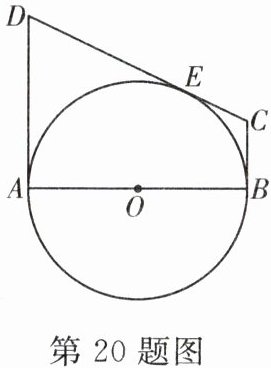
20. (10分)如图,$ AB $ 是 $ \odot O $ 的直径,$ AD $ 和 $ BC $ 分别切 $ \odot O $ 于 $ A $,$ B $ 两点,$ CD $ 与 $ \odot O $ 有公共点 $ E $,且 $ AD = DE $。
(1)求证：$ CD $ 是 $ \odot O $ 的切线；
(2)若 $ AB = 12 $,$ BC = 4 $,求 $ AD $ 的长。

答案：
解:
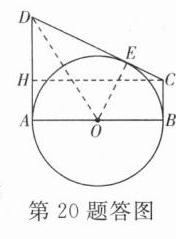
(1)证明:如答图，连接OD,OE,

∵AD切⊙O于点A,AB是⊙O的直径，
∴∠DAB = 90°.
∵AD = DE,OA = OE,OD = OD,
∴△ADO ≌ △EDO(SSS).
∴∠OED = ∠OAD = 90°，即OE⊥CD.又
∵OE是⊙O的半径，
∴CD是⊙O的切线.　
(2)解:如答图,过点C作CH⊥AD于点H.
∵AB是⊙O的直径，AD和BC分别切⊙O于A,B两点，
∴∠DAB = ∠ABC = ∠CHA = 90°.
∴四边形ABCH是矩形.
∴CH = AB = 12,AH = BC = 4.
∴DH = AD − AH = AD − 4,
∵CB,CD是⊙O的切线，
∴CE = BC = 4.又
∵AD = DE,
∴CD = AD + 4.
∵CH² + DH² = CD²,
∴12² + (AD − 4)² = (AD + 4)².
∴AD = 9.