《2025年三维数字课堂九年级数学上册人教版》

7. 如图,在 $ Rt\triangle ABC $ 中,$ \angle ACB = 90° $,$ \angle ABC = 30° $,将 $ \triangle ABC $ 绕点 $ C $ 顺时针旋转至 $ \triangle A'B'C $,使得点 $ A' $ 恰好落在 $ AB $ 上,则旋转角度为(B)

A.$ 30° $
B.$ 60° $
C.$ 90° $
D.$ 150° $

答案： B

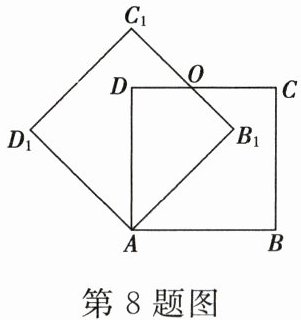
8. 如图,边长为1的正方形 $ ABCD $ 绕点 $ A $ 逆时针旋转 $ 45° $ 后得到正方形 $ AB_1C_1D_1 $,边 $ B_1C_1 $ 与 $ CD $ 交于点 $ O $,则四边形 $ AB_1OD $ 的面积是(D)

A.$ \frac{3}{4} $
B.$ \frac{7}{16} $
C.$ \frac{\sqrt{2}-1}{2} $
D.$ \sqrt{2}-1 $

答案： D

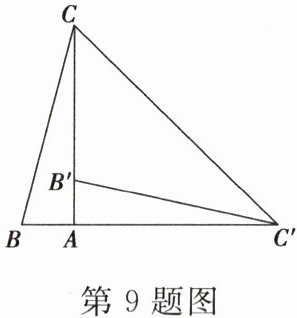
9. 如图,在 $ Rt\triangle ABC $ 中,$ \angle BAC = 90° $,将 $ \triangle ABC $ 绕点 $ A $ 顺时针旋转 $ 90° $ 后得到的 $ \triangle AB'C' $(点 $ B $ 的对应点是点 $ B' $,点 $ C $ 的对应点是点 $ C' $),连接 $ CC' $,若 $ \angle CC'B' = 32° $,则 $ \angle B $ 的大小是(C)

A.$ 32° $
B.$ 64° $
C.$ 77° $
D.$ 87° $

答案： C

10. 一副三角板叠在一起如图放置,最小锐角的顶点 $ D $ 恰好放在等腰直角三角形的斜边上,$ AC $ 与 $ DM $,$ DN $ 分别交于点 $ E $,$ F $,把 $ \triangle DEF $ 绕点 $ D $ 旋转到一定位置,使得 $ DE = DF $,则 $ \angle BDN $ 的度数是(C)

A.$ 105° $
B.$ 115° $
C.$ 120° $
D.$ 135° $

答案： C

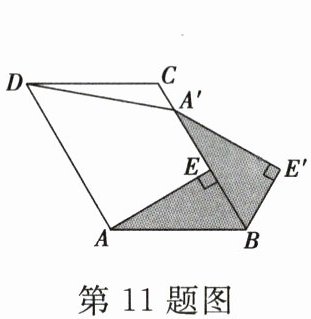
11. 如图,已知在 $ □ ABCD $ 中,$ AE \perp BC $ 于点 $ E $,以点 $ B $ 为中心,取旋转角等于 $ \angle ABC $,把 $ \triangle BAE $ 顺时针旋转得到 $ \triangle BA'E' $,连接 $ DA' $,若 $ \angle ADC = 60° $,$ \angle ADA' = 50° $,则 $ \angle DA'E' $ 的大小为(C)

A.$ 130° $
B.$ 150° $
C.$ 160° $
D.$ 170° $

答案： C

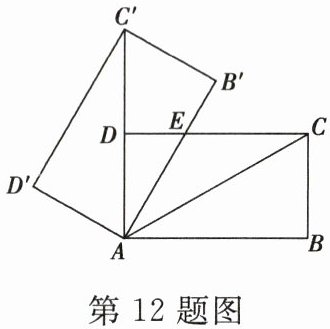
12. 如图,将矩形 $ ABCD $ 绕点 $ A $ 旋转至矩形 $ AB'C'D' $ 的位置,此时 $ AC $ 的中点恰好与点 $ D $ 重合,$ AB' $ 交 $ CD $ 于点 $ E $。若 $ AB = 3 $,则 $ \triangle AEC $ 的面积为(D)

A.3
B.1.5
C.$ 2\sqrt{3} $
D.$ \sqrt{3} $

答案： D 点拨：
∵旋转后 AC 的中点恰好与 D点重合，即$AD=\frac {1}{2}AC'=\frac {1}{2}AC$，
∴在$Rt△ACD$中,$∠ACD=30^{\circ }$，即$∠DAC=$$60^{\circ },\therefore ∠C'AD'=60^{\circ },\therefore ∠DAE=30^{\circ },$$\therefore ∠EAC=∠ACD=30^{\circ },\therefore AE=CE$.在$Rt△ADE$中，设$AE=EC=x$，则有$DE=$$DC-EC=AB-EC=3-x,AD=\frac {\sqrt {3}}{3}×$$3=\sqrt {3}$，根据勾股定理得$x^{2}=(3-x)^{2}+$$(\sqrt {3})^{2}$，解得$x=2,\therefore EC=2,\therefore S_{△AEC}=$$\frac {1}{2}EC\cdot AD=\sqrt {3}$，故选 D.

13. 在平面直角坐标系中,点 $ A(-2,-3) $ 关于原点对称的点 $ B $ 的坐标是(2,3)。

答案： (2,3)

14. 在平面直角坐标系中,以原点为中心,把点 $ A(4,5) $ 逆时针旋转 $ 90° $ 得到的点 $ B $ 的坐标为(-5,4)。

答案： (-5,4)