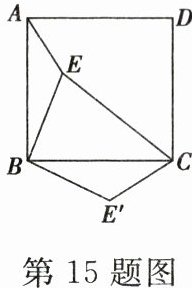
15. 如图,点 $ E $ 是正方形 $ ABCD $ 内一点,连接 $ AE $、$ BE $、$ CE $,将 $ \triangle ABE $ 绕点 $ B $ 顺时针旋转 $ 90° $ 到 $ \triangle CBE' $ 的位置,若 $ AE = 1 $,$ BE = 2 $,$ CE = 3 $,则 $ \angle BE'C = $
135
度。
答案:
135
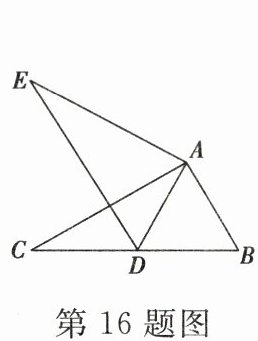
16. 如图,在 $ \triangle ABC $ 中,$ AB = 2 $,$ BC = 3.6 $,$ \angle B = 60° $,将 $ \triangle ABC $ 绕点 $ A $ 按顺时针旋转一定的角度得到 $ \triangle ADE $,当点 $ B $ 的对应点 $ D $ 恰好落在 $ BC $ 边上时,则 $ CD $ 的长为
1.6
。
答案:
1.6
17. 如图,在 $ Rt\triangle ABC $ 中,$ \angle ACB = 90° $,$ AC = 5\,cm $,$ BC = 12\,cm $,将 $ \triangle ABC $ 绕点 $ B $ 顺时针旋转 $ 60° $ 得到 $ \triangle BDE $,连接 $ DC $ 交 $ AB $ 于点 $ F $,则 $ \triangle ACF $ 与 $ \triangle BDF $ 的周长之和为

42
$cm$。
答案:
42
18. 如图,在 $ \triangle ABC $ 中,$ \angle A = 70° $,$ AC = BC $,以点 $ B $ 为旋转中心,把 $ \triangle ABC $ 按顺时针旋转 $ \alpha $ 度,得到 $ \triangle A'BC' $,点 $ A' $ 恰好落在 $ AC $ 上,连接 $ CC' $,则 $ \angle ACC' = $

110°
。
答案:
110° 点拨:$\because ∠A=70^{\circ },AC=BC,$$\therefore ∠BCA=40^{\circ }$.根据旋转的性质,可知$AB=BA',BC=BC',\therefore ∠α=180^{\circ }-2×$$70^{\circ }=40^{\circ }.\because ∠CBC'=∠α=40^{\circ },$$\therefore ∠BCC'=70^{\circ },\therefore ∠ACC'=∠ACB+$$∠BCC'=110^{\circ }.$
19. (10分)如图,在平面直角坐标系 $ xOy $ 中,点 $ A $ 的坐标为 $ (-2,0) $,等边三角形 $ AOC $ 经过平移或轴对称或旋转都可以得到 $ \triangle OBD $。
(1)$ \triangle AOC $ 沿 $ x $ 轴向右平移得到 $ \triangle OBD $,则平移的距离是
(2)连接 $ AD $,交 $ OC $ 于点 $ E $,求 $ \angle AEO $ 的度数。

(2)
∵等边$△AOC$绕原点 O 顺时针旋转$120^{\circ }$得到$△DOB,\therefore OA=OD.\because ∠AOC=$$∠BOD=60^{\circ },\therefore ∠DOC=60^{\circ }$,即 OE 为等腰$△AOD$的顶角的平分线,
∴OE 垂直平分AD,$\therefore ∠AEO=90^{\circ }.$
(1)$ \triangle AOC $ 沿 $ x $ 轴向右平移得到 $ \triangle OBD $,则平移的距离是
2
个单位长度;$ \triangle AOC $ 与 $ \triangle BOD $ 关于直线对称,则对称轴是y轴
;$ \triangle AOC $ 绕原点 $ O $ 顺时针旋转得到 $ \triangle DOB $,则旋转角度可以是120
度;(2)连接 $ AD $,交 $ OC $ 于点 $ E $,求 $ \angle AEO $ 的度数。

(2)
∵等边$△AOC$绕原点 O 顺时针旋转$120^{\circ }$得到$△DOB,\therefore OA=OD.\because ∠AOC=$$∠BOD=60^{\circ },\therefore ∠DOC=60^{\circ }$,即 OE 为等腰$△AOD$的顶角的平分线,
∴OE 垂直平分AD,$\therefore ∠AEO=90^{\circ }.$
答案:
(1)2 y轴 120
(2)
∵等边$△AOC$绕原点 O 顺时针旋转$120^{\circ }$得到$△DOB,\therefore OA=OD.\because ∠AOC=$$∠BOD=60^{\circ },\therefore ∠DOC=60^{\circ }$,即 OE 为等腰$△AOD$的顶角的平分线,
∴OE 垂直平分AD,$\therefore ∠AEO=90^{\circ }.$
(1)2 y轴 120
(2)
∵等边$△AOC$绕原点 O 顺时针旋转$120^{\circ }$得到$△DOB,\therefore OA=OD.\because ∠AOC=$$∠BOD=60^{\circ },\therefore ∠DOC=60^{\circ }$,即 OE 为等腰$△AOD$的顶角的平分线,
∴OE 垂直平分AD,$\therefore ∠AEO=90^{\circ }.$
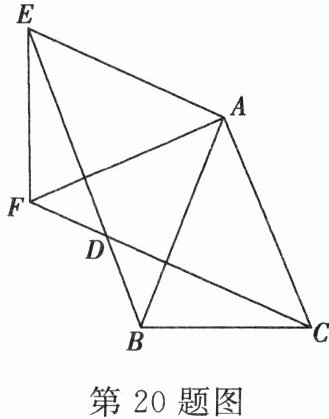
20. (10分)如图,在 $ \triangle ABC $ 中,$ AB = AC = 1 $,$ \angle BAC = 45° $,$ \triangle AEF $ 是由 $ \triangle ABC $ 绕点 $ A $ 按顺时针方向旋转得到的,连接 $ BE $、$ CF $ 相交于点 $ D $。
(1)求证:$ BE = CF $;
(2)当四边形 $ ACDE $ 为菱形时,求 $ BD $ 的长。
(1)求证:$ BE = CF $;
(2)当四边形 $ ACDE $ 为菱形时,求 $ BD $ 的长。

答案:
(1)证明:
∵$△AEF$是由$△ABC$绕点 A按顺时针方向旋转得到的,$\therefore AE=AB,$$AF=AC,∠EAF=∠BAC,\therefore ∠EAF+$$∠BAF=∠BAC+∠BAF$,即$∠EAB=$$∠FAC.\because AB=AC,\therefore AE=AF,$$\therefore △AEB$可由$△AFC$绕点 A 按顺时针方向旋转得到,$\therefore BE=CF.$
(2)解:
∵四边形 ACDE 为菱形,$AB=$$AC=1,\therefore DE=AE=AC=AB=1,AC//$$DE,\therefore ∠ABE=∠BAC=45^{\circ },$$\therefore ∠AEB=∠ABE=45^{\circ },\therefore △ABE$为等腰直角三角形,$\therefore BE=\sqrt {2}AC=\sqrt {2},\therefore BD=$$BE-DE=\sqrt {2}-1.$
(1)证明:
∵$△AEF$是由$△ABC$绕点 A按顺时针方向旋转得到的,$\therefore AE=AB,$$AF=AC,∠EAF=∠BAC,\therefore ∠EAF+$$∠BAF=∠BAC+∠BAF$,即$∠EAB=$$∠FAC.\because AB=AC,\therefore AE=AF,$$\therefore △AEB$可由$△AFC$绕点 A 按顺时针方向旋转得到,$\therefore BE=CF.$
(2)解:
∵四边形 ACDE 为菱形,$AB=$$AC=1,\therefore DE=AE=AC=AB=1,AC//$$DE,\therefore ∠ABE=∠BAC=45^{\circ },$$\therefore ∠AEB=∠ABE=45^{\circ },\therefore △ABE$为等腰直角三角形,$\therefore BE=\sqrt {2}AC=\sqrt {2},\therefore BD=$$BE-DE=\sqrt {2}-1.$
查看更多完整答案,请扫码查看


