第50页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
1.【兰州】一只标有“6 V 3 W”字样的小灯泡L与一个阻值为8Ω的定值电阻R串联,接在电源电压恒定不变的电路中,接通电路后,小灯泡L恰好正常发光。求:
(1)电路中的电流I。
(2)电源电压U。
(3)通电20 s,整个电路消耗的电能W。
(1)电路中的电流I。
(2)电源电压U。
(3)通电20 s,整个电路消耗的电能W。
答案:
1.
(1)小灯泡正常发光,由P=UI得,此时通过小灯泡的电流$I=\frac{P_{L}}{U_{L}}=\frac{3\,W}{6\,V}=0.5\,A$,由于小灯泡与电阻串联,故$I=I_{L}=I_{R}=0.5\,A$。
(2)由$I=\frac{U}{R}$得,电阻两端电压$U_{R}=IR=0.5\,A×8\,\Omega = 4\,V$,因为串联电路中总电压等于各用电器两端的电压之和,故总电压$U=U_{L}+U_{R}=6\,V+4\,V=10\,V$。
(3)通电20s,整个电路消耗的电能$W=UIt=10\,V×0.5\,A×20\,s=100\,J$。
(1)小灯泡正常发光,由P=UI得,此时通过小灯泡的电流$I=\frac{P_{L}}{U_{L}}=\frac{3\,W}{6\,V}=0.5\,A$,由于小灯泡与电阻串联,故$I=I_{L}=I_{R}=0.5\,A$。
(2)由$I=\frac{U}{R}$得,电阻两端电压$U_{R}=IR=0.5\,A×8\,\Omega = 4\,V$,因为串联电路中总电压等于各用电器两端的电压之和,故总电压$U=U_{L}+U_{R}=6\,V+4\,V=10\,V$。
(3)通电20s,整个电路消耗的电能$W=UIt=10\,V×0.5\,A×20\,s=100\,J$。
2.【吉林】如图所示,$R_{1}$的电阻为5Ω,闭合开关S后,通过电阻$R_{1}和R_{2}$的电流分别为0.6 A和0.3 A,求:
(1)电源电压。
(2)整个电路消耗的总功率。
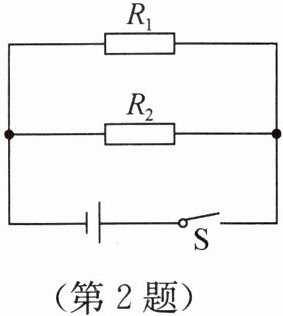
(1)电源电压。
(2)整个电路消耗的总功率。

答案:
2.
(1)由图知,$R_{1}$和$R_{2}$并联,$R_{1}$两端的电压$U_{1}=I_{1}R_{1}=0.6\,A×5\,\Omega = 3\,V$,由并联电路的电压特点可得电源电压$U=U_{1}=3\,V$。
(2)并联电路的总电流$I_{总}=I_{1}+I_{2}=0.6\,A+0.3\,A=0.9\,A$;则总功率$P_{总}=UI_{总}=3\,V×0.9\,A=2.7\,W$。
(1)由图知,$R_{1}$和$R_{2}$并联,$R_{1}$两端的电压$U_{1}=I_{1}R_{1}=0.6\,A×5\,\Omega = 3\,V$,由并联电路的电压特点可得电源电压$U=U_{1}=3\,V$。
(2)并联电路的总电流$I_{总}=I_{1}+I_{2}=0.6\,A+0.3\,A=0.9\,A$;则总功率$P_{总}=UI_{总}=3\,V×0.9\,A=2.7\,W$。
3.【湖州】方方用如图甲所示的电路研究电功率和电流的关系,绘制了定值电阻$R_{0}$、滑动变阻器R的功率与电流的关系图,如图乙所示。
(1)实线表示的是______(填“R”或“$R_{0}$”)的功率与电流的关系。
(2)求$R_{0}$的阻值。
(3)当电流表的示数为0.5 A时,求R消耗的功率。

(1)实线表示的是______(填“R”或“$R_{0}$”)的功率与电流的关系。
(2)求$R_{0}$的阻值。
(3)当电流表的示数为0.5 A时,求R消耗的功率。

答案:
3.
(1)$R_{0}$
(2)由图乙中,$R_{0}$的功率与电流的关系图像知,$I = 2\,A$时,$P_{0}=32\,W$,由$P = I^{2}R$可得,$R_{0}=\frac{P_{0}}{I_{0}^{2}}=\frac{32\,W}{(2\,A)^{2}}=8\,\Omega$。
(3)由电路图可知,定值电阻$R_{0}$与滑动变阻器R串联,当滑动变阻器R连入电路的阻值为0时,此时为$R_{0}$的简单电路,电路中电流最大,由图像知此时的电流$I = 2\,A$,由$P = UI$可得,电源电压$U = U_{0}=\frac{P_{0}}{I}=\frac{32\,W}{2\,A}=16\,V$,由欧姆定律可得,当电路中电流$I' = 0.5\,A$时,$R_{0}$两端电压$U_{0}' = I'R_{0}=0.5\,A×8\,\Omega = 4\,V$,由串联电路的特点知,此时R两端电压$U_{R}=U - U_{0}'=16\,V-4\,V=12\,V$,此时R消耗的功率$P_{R}=U_{R}I'=12\,V×0.5\,A=6\,W$。
(1)$R_{0}$
(2)由图乙中,$R_{0}$的功率与电流的关系图像知,$I = 2\,A$时,$P_{0}=32\,W$,由$P = I^{2}R$可得,$R_{0}=\frac{P_{0}}{I_{0}^{2}}=\frac{32\,W}{(2\,A)^{2}}=8\,\Omega$。
(3)由电路图可知,定值电阻$R_{0}$与滑动变阻器R串联,当滑动变阻器R连入电路的阻值为0时,此时为$R_{0}$的简单电路,电路中电流最大,由图像知此时的电流$I = 2\,A$,由$P = UI$可得,电源电压$U = U_{0}=\frac{P_{0}}{I}=\frac{32\,W}{2\,A}=16\,V$,由欧姆定律可得,当电路中电流$I' = 0.5\,A$时,$R_{0}$两端电压$U_{0}' = I'R_{0}=0.5\,A×8\,\Omega = 4\,V$,由串联电路的特点知,此时R两端电压$U_{R}=U - U_{0}'=16\,V-4\,V=12\,V$,此时R消耗的功率$P_{R}=U_{R}I'=12\,V×0.5\,A=6\,W$。
4.【长沙】为了更好地控制煎药时的火候,某厂家生产了一款全自动电煎药壶,它有“加热”和“保温”两个挡位,简化电路图如图所示,其中$S_{2}$是一个温控开关,温度过高时自动断开。
(1)当$S_{1}和S_{2}$闭合时,电煎药壶处于______挡位。
(2)电煎药壶在______挡位工作时,通过P点的电流更小。

(1)当$S_{1}和S_{2}$闭合时,电煎药壶处于______挡位。
(2)电煎药壶在______挡位工作时,通过P点的电流更小。

答案:
4.
(1)加热
(2)保温
(1)加热
(2)保温
5.【北京】如图所示为某款家用电热器的简化电路,$R_{1}$、$R_{2}$为阻值一定的电热丝。该电热器接入电压恒为220 V的电路中。电热器高温挡的功率为990 W,低温挡的功率为110 W。求:
(1)低温挡时通过电路的电流。
(2)电热丝$R_{2}$的阻值。

(1)低温挡时通过电路的电流。
(2)电热丝$R_{2}$的阻值。

答案:
5.
(1)当$S_{1}$闭合,$S_{2}$断开时,电热器处于低温挡,简化电路如图所示。

低温挡功率$P_{1}=110\,W$,故$I_{1}=\frac{P_{1}}{U}=\frac{110\,W}{220\,V}=0.5\,A$。
(2)当$S_{1}$、$S_{2}$都闭合时,电热器处于高温挡,简化电路如图所示。

电阻$R_{2}$的功率$P_{2}=P_{总}-P_{1}=990\,W-110\,W=880\,W$,电阻$R_{2}=\frac{U^{2}}{P_{2}}=\frac{(220\,V)^{2}}{880\,W}=55\,\Omega$。
5.
(1)当$S_{1}$闭合,$S_{2}$断开时,电热器处于低温挡,简化电路如图所示。

低温挡功率$P_{1}=110\,W$,故$I_{1}=\frac{P_{1}}{U}=\frac{110\,W}{220\,V}=0.5\,A$。
(2)当$S_{1}$、$S_{2}$都闭合时,电热器处于高温挡,简化电路如图所示。

电阻$R_{2}$的功率$P_{2}=P_{总}-P_{1}=990\,W-110\,W=880\,W$,电阻$R_{2}=\frac{U^{2}}{P_{2}}=\frac{(220\,V)^{2}}{880\,W}=55\,\Omega$。
查看更多完整答案,请扫码查看


