(1)半径是 4 dm 的圆,它的周长是
25.12
dm,面积是50.24
dm²,把这个圆的半径扩大到原来的 3 倍,则周长扩大到原来的3
倍,面积扩大到原来的9
倍。
答案:
解析:
本题考查圆的周长和面积的计算,以及半径变化对周长和面积的影响。
首先,我们需要使用圆的周长公式 $C = 2\pi r$ 和面积公式 $S = \pi r^2$ 来计算原始圆的周长和面积。
然后,我们考虑半径扩大到原来的3倍时,周长和面积如何变化。
新的半径 $r' = 3r = 3 × 4 = 12(dm)$。
新的周长 $C' = 2\pi r' = 2\pi × 12 = 24\pi (dm)$,是原来周长的3倍。
新的面积 $S' = \pi (r')^2 = \pi × 12^2 = 144\pi (dm^2)$,是原来面积的9倍。
答案:
半径是 4 dm 的圆,它的周长是$(2\pi × 4 = 8\pi \approx 25.12)(dm)$,
面积是$(\pi × 4^2 = 16\pi \approx 50.24)(dm^2)$,
把这个圆的半径扩大到原来的 3 倍,则周长扩大到原来的(3)倍,
面积扩大到原来的(9)倍。
本题考查圆的周长和面积的计算,以及半径变化对周长和面积的影响。
首先,我们需要使用圆的周长公式 $C = 2\pi r$ 和面积公式 $S = \pi r^2$ 来计算原始圆的周长和面积。
然后,我们考虑半径扩大到原来的3倍时,周长和面积如何变化。
新的半径 $r' = 3r = 3 × 4 = 12(dm)$。
新的周长 $C' = 2\pi r' = 2\pi × 12 = 24\pi (dm)$,是原来周长的3倍。
新的面积 $S' = \pi (r')^2 = \pi × 12^2 = 144\pi (dm^2)$,是原来面积的9倍。
答案:
半径是 4 dm 的圆,它的周长是$(2\pi × 4 = 8\pi \approx 25.12)(dm)$,
面积是$(\pi × 4^2 = 16\pi \approx 50.24)(dm^2)$,
把这个圆的半径扩大到原来的 3 倍,则周长扩大到原来的(3)倍,
面积扩大到原来的(9)倍。
(2)一个圆环,外圆半径是 3 cm,内圆半径是 2 cm,这个圆环的面积是
15.7
$cm^2。$
答案:
解析:本题考查圆环的面积计算。需要用到圆的面积公式$S = \pi r^2$,圆环的面积等于外圆的面积减去内圆的面积。
外圆半径$R = 3cm$,外圆面积$S_1 = \pi R^2 = \pi × 3^2 = 9\pi$($cm^2$);
内圆半径$r = 2cm$,内圆面积$S_2 = \pi r^2 = \pi × 2^2 = 4\pi$($cm^2$);
圆环面积$S = S_1 - S_2 = 9\pi - 4\pi = 5\pi$($cm^2$),$\pi$取$3.14$,则$S = 5 × 3.14 = 15.7$($cm^2$)。
答案:$15.7$。
外圆半径$R = 3cm$,外圆面积$S_1 = \pi R^2 = \pi × 3^2 = 9\pi$($cm^2$);
内圆半径$r = 2cm$,内圆面积$S_2 = \pi r^2 = \pi × 2^2 = 4\pi$($cm^2$);
圆环面积$S = S_1 - S_2 = 9\pi - 4\pi = 5\pi$($cm^2$),$\pi$取$3.14$,则$S = 5 × 3.14 = 15.7$($cm^2$)。
答案:$15.7$。
(3)一个半圆的半径是 1 cm,它的周长是(
5.14
)cm,面积是(1.57
)$cm^2。$
答案:
解析:
题目考查半圆的周长和面积计算。
首先,半圆的周长由半圆弧和直径组成。
半圆弧的长度是圆周长的一半,即$\pi r$,其中$r$是半径。
直径的长度是$2r$。
因此,半圆的周长计算公式是$\pi r + 2r$。
将半径$r=1 \text{cm}$代入公式,得到周长为$\pi × 1 + 2 × 1 = \pi + 2 \approx 5.14 \text{cm}$。
接下来,半圆的面积是圆面积的一半。
圆的面积计算公式是$\pi r^2$。
因此,半圆的面积是$\frac{1}{2} \pi r^2$。
将半径$r=1 \text{cm}$代入公式,得到面积为$\frac{1}{2} \pi × 1^2 = \frac{1}{2} \pi \approx 1.57 \text{cm}^2$。
答案:
(3)一个半圆的半径是$1 \text{cm}$,它的周长是$(5.14)\text{cm}$,面积是$(1.57)\text{cm}^2$。
题目考查半圆的周长和面积计算。
首先,半圆的周长由半圆弧和直径组成。
半圆弧的长度是圆周长的一半,即$\pi r$,其中$r$是半径。
直径的长度是$2r$。
因此,半圆的周长计算公式是$\pi r + 2r$。
将半径$r=1 \text{cm}$代入公式,得到周长为$\pi × 1 + 2 × 1 = \pi + 2 \approx 5.14 \text{cm}$。
接下来,半圆的面积是圆面积的一半。
圆的面积计算公式是$\pi r^2$。
因此,半圆的面积是$\frac{1}{2} \pi r^2$。
将半径$r=1 \text{cm}$代入公式,得到面积为$\frac{1}{2} \pi × 1^2 = \frac{1}{2} \pi \approx 1.57 \text{cm}^2$。
答案:
(3)一个半圆的半径是$1 \text{cm}$,它的周长是$(5.14)\text{cm}$,面积是$(1.57)\text{cm}^2$。
(4)圆心角是 45°的扇形的面积是其所在圆面积的$\frac{
1
}{8
}$。
答案:
解析:
一个完整的圆的圆心角是$360^\circ$。
扇形的面积占其所在圆面积的比例等于扇形的圆心角占整个圆$360^\circ$的比例。
因此,圆心角是$45^\circ$的扇形的面积占其所在圆面积的比例为:
$\frac{45^\circ}{360^\circ}$。
计算这个比例,得到:
$\frac{45}{360} = \frac{1}{8}$。
答案:
$\frac{1}{8}$。
一个完整的圆的圆心角是$360^\circ$。
扇形的面积占其所在圆面积的比例等于扇形的圆心角占整个圆$360^\circ$的比例。
因此,圆心角是$45^\circ$的扇形的面积占其所在圆面积的比例为:
$\frac{45^\circ}{360^\circ}$。
计算这个比例,得到:
$\frac{45}{360} = \frac{1}{8}$。
答案:
$\frac{1}{8}$。
(5)甲圆半径与乙圆直径相等,那么乙圆面积是甲圆面积的$\frac{
1
}{4
}$。
答案:
解析:本题考查圆的面积公式以及分数表示。
设甲圆的半径为 $r$,则甲圆的面积为 $S_{甲}=\pi r^{2}$。
因为乙圆的直径等于甲圆的半径,所以乙圆的半径为$\frac{r}{2}$,那么乙圆的面积 $S_{乙}$ 可以通过圆的面积公式计算得出:
$S_{乙} = \pi \left(\frac{r}{2}\right)^{2} = \pi × \frac{r^{2}}{4} = \frac{\pi r^{2}}{4}$,
接下来求乙圆面积与甲圆面积的比例:
$\frac{S_{乙}}{S_{甲}} = \frac{\frac{\pi r^{2}}{4}}{\pi r^{2}} = \frac{1}{4}$,
答案:$\frac{1}{4}$。
设甲圆的半径为 $r$,则甲圆的面积为 $S_{甲}=\pi r^{2}$。
因为乙圆的直径等于甲圆的半径,所以乙圆的半径为$\frac{r}{2}$,那么乙圆的面积 $S_{乙}$ 可以通过圆的面积公式计算得出:
$S_{乙} = \pi \left(\frac{r}{2}\right)^{2} = \pi × \frac{r^{2}}{4} = \frac{\pi r^{2}}{4}$,
接下来求乙圆面积与甲圆面积的比例:
$\frac{S_{乙}}{S_{甲}} = \frac{\frac{\pi r^{2}}{4}}{\pi r^{2}} = \frac{1}{4}$,
答案:$\frac{1}{4}$。
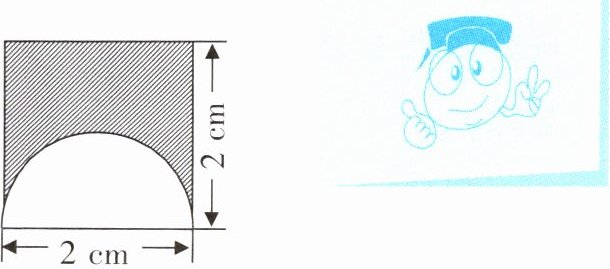
(6)求图中阴影部分的周长和面积。

答案:
解析:本题主要考查圆的周长和面积公式,以及长方形的周长和面积公式,通过观察图形可知,阴影部分的周长等于长方形的两条长加一条宽的长度再加上半圆的弧长;阴影部分的面积等于长方形的面积减去半圆的面积。
计算阴影部分的周长:
已知长方形的长为$2cm$,宽为$2cm$,半圆的直径为$2cm$,那么半径$r = 2÷2 = 1cm$。
圆的周长公式为$C = 2\pi r$($C$表示圆的周长,$\pi$通常取$3.14$,$r$为半径),则半圆的弧长为$\frac{1}{2}×2×3.14×1 = 3.14cm$。
长方形的两条长加一条宽的长度为$2×2 + 2 = 6cm$。
所以阴影部分的周长为$6 + 3.14 = 9.14cm$。
计算阴影部分的面积:
长方形的面积公式为$S_{长}=长×宽$,则长方形的面积为$2×2 = 4cm^{2}$。
圆的面积公式为$S = \pi r^{2}$,则半圆的面积为$\frac{1}{2}×3.14×1^{2} = 1.57cm^{2}$。
所以阴影部分的面积为$4 - 1.57 = 2.43cm^{2}$。
答案:周长$9.14cm$,面积$2.43cm^{2}$。
计算阴影部分的周长:
已知长方形的长为$2cm$,宽为$2cm$,半圆的直径为$2cm$,那么半径$r = 2÷2 = 1cm$。
圆的周长公式为$C = 2\pi r$($C$表示圆的周长,$\pi$通常取$3.14$,$r$为半径),则半圆的弧长为$\frac{1}{2}×2×3.14×1 = 3.14cm$。
长方形的两条长加一条宽的长度为$2×2 + 2 = 6cm$。
所以阴影部分的周长为$6 + 3.14 = 9.14cm$。
计算阴影部分的面积:
长方形的面积公式为$S_{长}=长×宽$,则长方形的面积为$2×2 = 4cm^{2}$。
圆的面积公式为$S = \pi r^{2}$,则半圆的面积为$\frac{1}{2}×3.14×1^{2} = 1.57cm^{2}$。
所以阴影部分的面积为$4 - 1.57 = 2.43cm^{2}$。
答案:周长$9.14cm$,面积$2.43cm^{2}$。
查看更多完整答案,请扫码查看


