《2025年口算训练宁波出版社六年级数学上册人教版》

1. 填空。
(1)$ r= 1\ \text{cm} $
$ S= $3.14$\text{cm}^2 $
(2)$ d= 20\ \text{m} $
$ S= $314$\text{m}^2 $
(3)$ r= 2\ \text{dm} $
$ S= $12.56$\text{dm}^2 $
(4)$ r= 3\ \text{dm} $
$ S= $28.26$\text{dm}^2 $
(5)$ d= 10\ \text{m} $
$ S= $78.5$\text{m}^2 $
(6)$ r= 0.1\ \text{dm} $
$ S= $0.0314$\text{dm}^2 $
(7)$ d= 6\ \text{cm} $
$ S= $28.26$\text{cm}^2 $
(8)$ d= 200\ \text{cm} $
$ S= $31400$\text{cm}^2 $
(9)$ r= 4\ \text{cm} $
$ S= $50.24$\text{cm}^2 $
(10)$ r= 5\ \text{m} $
$ S= $78.5$\text{m}^2 $

答案： 解析：本题考查圆的面积公式，$S=\pi r^2$，其中$r$为半径，$d$为直径，所以$r=\frac{d}{2}$。
(1)$r=1\text{cm}$，$S = \pi × 1^2=\pi\approx3.14\text{cm}^2$。
答案：$3.14$。
(2)$d=20\text{m}$，$r = 10\text{m}$，$S=\pi × 10^2 = 100\pi\approx314\text{m}^2$。
答案：$314$。
(3)$r=2\text{dm}$，$S=\pi × 2^2 = 4\pi\approx12.56\text{dm}^2$。
答案：$12.56$。
(4)$r=3\text{dm}$，$S=\pi × 3^2=9\pi\approx28.26\text{dm}^2$。
答案：$28.26$。
(5)$d=10\text{m}$，$r = 5\text{m}$，$S=\pi × 5^2=25\pi\approx78.5\text{m}^2$。
答案：$78.5$。
(6)$r=0.1\text{dm}$，$S=\pi × 0.1^2 = 0.01\pi\approx0.0314\text{dm}^2$。
答案：$0.0314$。
(7)$d=6\text{cm}$，$r = 3\text{cm}$，$S=\pi × 3^2 = 9\pi\approx28.26\text{cm}^2$。
答案：$28.26$。
(8)$d=200\text{cm}$，$r = 100\text{cm}$，$S=\pi × 100^2=10000\pi\approx31400\text{cm}^2$。
答案：$31400$。
(9)$r=4\text{cm}$，$S=\pi × 4^2=16\pi\approx50.24\text{cm}^2$。
答案：$50.24$。
(10)$r=5\text{m}$，$S=\pi × 5^2=25\pi\approx78.5\text{m}^2$。
答案：$78.5$。

2. 计算下面圆或圆环的面积。
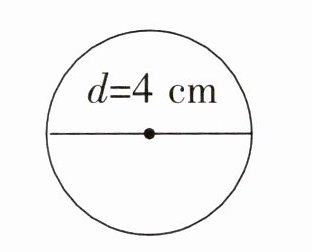
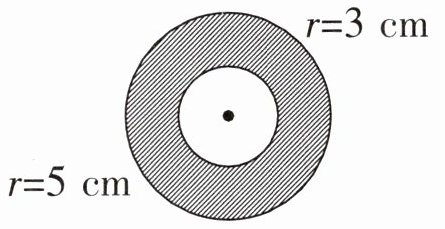
(1)
(2)

答案： 解析：本题主要考查圆的面积公式。圆的面积公式为$S = \pi r^{2}$（$S$表示圆的面积，$r$表示圆的半径，$\pi$通常取$3.14$）。对于圆环，其面积等于外圆面积减去内圆面积，即$S_{环}=\pi R^{2}-\pi r^{2}$（$R$为外圆半径，$r$为内圆半径）。
(1) 由图可知圆的直径$d = 4$cm，根据半径与直径的关系$r=\frac{d}{2}$，可得半径$r = 4÷2 = 2$cm。
再根据圆的面积公式$S = \pi r^{2}$，$\pi$取$3.14$，则该圆的面积为：
$S = 3.14×2^{2}=3.14×4 = 12.56$($cm^{2}$)。
所以本题答案为$12.56cm^{2}$。
(2) 由图可知外圆半径$R = 5$cm，内圆半径$r = 3$cm。
根据圆环面积公式$S_{环}=\pi R^{2}-\pi r^{2}$，$\pi$取$3.14$，可得：
$S_{环}=3.14×(5^{2}-3^{2})$
$=3.14×(25 - 9)$
$=3.14×16$
$ = 50.24$($cm^{2}$)。
所以本题答案为$50.24cm^{2}$。