例2 解决问题。
(1)部分与总体问题
小明用10元钱买了4支圆珠笔,找回0.48元,每支圆珠笔多少元?
【解答】$(10-0.48)÷4= 2.38$(元)
答:每支圆珠笔2.38元。
(2)倍数问题
果园里有桃树150棵,比杏树的2倍少50棵,杏树有多少棵?
【解答】$(150+50)÷2= 100$(棵)
答:杏树有100棵。
温馨提示:倍数问题,当标准量不知道时,用算术方法解答很容易出错,建议最好用方程解答。
(3)相遇问题
甲、乙两辆汽车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米。两车在距中点32千米处相遇。东、西两地相距多少千米?
【解答】$32×2÷(56-48)= 8$(小时) $(56+48)×8= 832$(千米)
答:东、西两地相距832千米。
(4)鸡兔同笼问题
鸡兔同笼,有17个头,42条腿,鸡、兔各有多少只?
【解答】方法一:
|头/个|鸡/只|兔/只|腿/条|
|17|9|8|50|
|17|10|7|48|
|17|11|6|46|
|17|12|5|44|
|17|13|4|42|
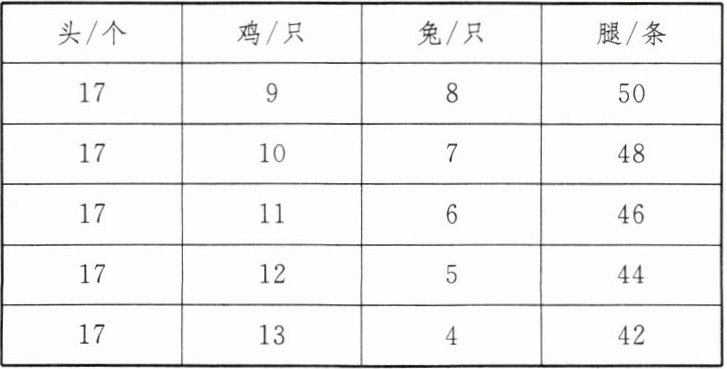
答:鸡有13只,兔有4只。
方法二:假设鸡笼里全是鸡 $42-17×2= 8$(条) 兔:$8÷(4-2)= 4$(只) 鸡:$17-4= 13$(只)
答:兔有4只,鸡有13只。
温馨提示:鸡兔同笼问题,也可以用方程解答。
(5)分数应用题
一辆汽车从甲地开往乙地,第一小时行了全程的$\frac{1}{7}$,第二小时比第一小时多行了16千米,这时距离乙地还有94千米。甲、乙两地间的公路长多少千米?
【解答】方法一:$(94+16)÷(1-\frac{1}{7}-\frac{1}{7})= 154$(千米)
答:甲、乙两地间的公路长154千米。
方法二:设全程为$x$千米。
$x-\frac{1}{7}x-\frac{1}{7}x-16= 94$ $x= 154$
答:甲、乙两地间的公路长154千米。
(6)按比例分配问题
光明小学将五年级的140名学生分成三个小组进行植树活动。已知第一小组和第二小组人数的比是$2:3$,第二小组和第三小组人数的比是$4:5$。这三个小组各有多少人?
【解答】第一、二小组人数的比是$2:3$,第二、三小组人数的比是$4:5$,因为在两条信息中,第二小组所占的份数不一致,所以要将第二小组的份数进行统一,因此将第二小组的份数变为12,则第一小组变为8,第三小组变为15,第一、二、三小组人数的比是$8:12:15$。
总份数:$8+12+15= 35$
第一小组:$140×\frac{8}{35}= 32$(人)
第二小组:$140×\frac{12}{35}= 48$(人)
第三小组:$140×\frac{15}{35}= 60$(人)
答:第一小组有32人,第二小组有48人,第三小组有60人。
(7)求利息的问题
淘气计划将今年得到的2000元存入银行,定期三年,准备到期后将利息捐给“希望工程”。若年利率按3.69%计算,3年后,淘气给“希望工程”捐了多少钱?
【解答】$2000×3.69\%×3= 221.4$(元)
答:淘气给“希望工程”捐了221.4元。
(1)部分与总体问题
小明用10元钱买了4支圆珠笔,找回0.48元,每支圆珠笔多少元?
【解答】$(10-0.48)÷4= 2.38$(元)
答:每支圆珠笔2.38元。
(2)倍数问题
果园里有桃树150棵,比杏树的2倍少50棵,杏树有多少棵?
【解答】$(150+50)÷2= 100$(棵)
答:杏树有100棵。
温馨提示:倍数问题,当标准量不知道时,用算术方法解答很容易出错,建议最好用方程解答。
(3)相遇问题
甲、乙两辆汽车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米。两车在距中点32千米处相遇。东、西两地相距多少千米?
【解答】$32×2÷(56-48)= 8$(小时) $(56+48)×8= 832$(千米)
答:东、西两地相距832千米。
(4)鸡兔同笼问题
鸡兔同笼,有17个头,42条腿,鸡、兔各有多少只?
【解答】方法一:
|头/个|鸡/只|兔/只|腿/条|
|17|9|8|50|
|17|10|7|48|
|17|11|6|46|
|17|12|5|44|
|17|13|4|42|

答:鸡有13只,兔有4只。
方法二:假设鸡笼里全是鸡 $42-17×2= 8$(条) 兔:$8÷(4-2)= 4$(只) 鸡:$17-4= 13$(只)
答:兔有4只,鸡有13只。
温馨提示:鸡兔同笼问题,也可以用方程解答。
(5)分数应用题
一辆汽车从甲地开往乙地,第一小时行了全程的$\frac{1}{7}$,第二小时比第一小时多行了16千米,这时距离乙地还有94千米。甲、乙两地间的公路长多少千米?
【解答】方法一:$(94+16)÷(1-\frac{1}{7}-\frac{1}{7})= 154$(千米)
答:甲、乙两地间的公路长154千米。
方法二:设全程为$x$千米。
$x-\frac{1}{7}x-\frac{1}{7}x-16= 94$ $x= 154$
答:甲、乙两地间的公路长154千米。
(6)按比例分配问题
光明小学将五年级的140名学生分成三个小组进行植树活动。已知第一小组和第二小组人数的比是$2:3$,第二小组和第三小组人数的比是$4:5$。这三个小组各有多少人?
【解答】第一、二小组人数的比是$2:3$,第二、三小组人数的比是$4:5$,因为在两条信息中,第二小组所占的份数不一致,所以要将第二小组的份数进行统一,因此将第二小组的份数变为12,则第一小组变为8,第三小组变为15,第一、二、三小组人数的比是$8:12:15$。
总份数:$8+12+15= 35$
第一小组:$140×\frac{8}{35}= 32$(人)
第二小组:$140×\frac{12}{35}= 48$(人)
第三小组:$140×\frac{15}{35}= 60$(人)
答:第一小组有32人,第二小组有48人,第三小组有60人。
(7)求利息的问题
淘气计划将今年得到的2000元存入银行,定期三年,准备到期后将利息捐给“希望工程”。若年利率按3.69%计算,3年后,淘气给“希望工程”捐了多少钱?
【解答】$2000×3.69\%×3= 221.4$(元)
答:淘气给“希望工程”捐了221.4元。
答案:
(1)$(10-0.48)÷4=2.38$(元)
答:每支圆珠笔2.38元。
(2)$(150+50)÷2=100$(棵)
答:杏树有100棵。
(3)$32×2÷(56-48)=8$(小时)
$(56+48)×8=832$(千米)
答:东、西两地相距832千米。
(4)方法一:
|头/个|鸡/只|兔/只|腿/条|
|----|----|----|----|
|17|9|8|50|
|17|10|7|48|
|17|11|6|46|
|17|12|5|44|
|17|13|4|42|
答:鸡有13只,兔有4只。
方法二:$42-17×2=8$(条)
兔:$8÷(4-2)=4$(只)
鸡:$17-4=13$(只)
答:兔有4只,鸡有13只。
(5)方法一:$(94+16)÷(1-\frac{1}{7}-\frac{1}{7})=154$(千米)
答:甲、乙两地间的公路长154千米。
方法二:设全程为$x$千米。
$x-\frac{1}{7}x-\frac{1}{7}x-16=94$
$x=154$
答:甲、乙两地间的公路长154千米。
(6)第一、二小组人数的比是$2:3=8:12$,第二、三小组人数的比是$4:5=12:15$,所以第一、二、三小组人数的比是$8:12:15$。
总份数:$8+12+15=35$
第一小组:$140×\frac{8}{35}=32$(人)
第二小组:$140×\frac{12}{35}=48$(人)
第三小组:$140×\frac{15}{35}=60$(人)
答:第一小组有32人,第二小组有48人,第三小组有60人。
(7)$2000×3.69\%×3=221.4$(元)
答:淘气给“希望工程”捐了221.4元。
(1)$(10-0.48)÷4=2.38$(元)
答:每支圆珠笔2.38元。
(2)$(150+50)÷2=100$(棵)
答:杏树有100棵。
(3)$32×2÷(56-48)=8$(小时)
$(56+48)×8=832$(千米)
答:东、西两地相距832千米。
(4)方法一:
|头/个|鸡/只|兔/只|腿/条|
|----|----|----|----|
|17|9|8|50|
|17|10|7|48|
|17|11|6|46|
|17|12|5|44|
|17|13|4|42|
答:鸡有13只,兔有4只。
方法二:$42-17×2=8$(条)
兔:$8÷(4-2)=4$(只)
鸡:$17-4=13$(只)
答:兔有4只,鸡有13只。
(5)方法一:$(94+16)÷(1-\frac{1}{7}-\frac{1}{7})=154$(千米)
答:甲、乙两地间的公路长154千米。
方法二:设全程为$x$千米。
$x-\frac{1}{7}x-\frac{1}{7}x-16=94$
$x=154$
答:甲、乙两地间的公路长154千米。
(6)第一、二小组人数的比是$2:3=8:12$,第二、三小组人数的比是$4:5=12:15$,所以第一、二、三小组人数的比是$8:12:15$。
总份数:$8+12+15=35$
第一小组:$140×\frac{8}{35}=32$(人)
第二小组:$140×\frac{12}{35}=48$(人)
第三小组:$140×\frac{15}{35}=60$(人)
答:第一小组有32人,第二小组有48人,第三小组有60人。
(7)$2000×3.69\%×3=221.4$(元)
答:淘气给“希望工程”捐了221.4元。
查看更多完整答案,请扫码查看


