《2025年名校课堂八年级数学上册冀教版河北专版》

12. (2024·石家庄 44 中期中)已知 $A = \frac{x^{2}-9}{x^{2}+6x + 9} ÷ \frac{x}{x + 3}$，则关于甲、乙、丙的说法，下列判断正确的是(C)
甲：$A$ 的计算结果为 $\frac{x - 3}{x}$；
乙：当 $x = -3$ 时，$A = 2$；
丙：当 $0 ＜ x ＜ 3$ 时，$A$ 的值为正数。

A.乙错，丙对
B.甲和乙都对
C.甲对，丙错
D.甲错，丙对

答案： 12.C

13. 一个水平放置的长方体容器，其容积为 $V$，底面的长为 $a$，宽为 $b$，当容器内的水占容积的 $\frac{m}{n}$ 时，水面的高度为$\frac{mV}{nab}$。

答案： 13.$\frac {mV}{nab}$

14. 计算：
(1) $(-\frac{2a}{b^{2}})^{3} \cdot (\frac{2b}{a})^{2} ÷ (-\frac{2b}{a})^{2}$；
(2) $\frac{x^{2}+xy}{x^{2}-xy} ÷ (x + y) \cdot \frac{y^{2}-xy}{-xy}$。

答案： 14.解:
(1)原式$=-\frac {8a^{3}}{b^{6}}\cdot \frac {4b^{2}}{a^{2}}÷\frac {4b^{2}}{a^{2}}=-\frac {8a^{3}}{b^{6}}\cdot \frac {4b^{2}}{a^{2}}\cdot \frac {a^{2}}{4b^{2}}=-\frac {8a^{3}}{b^{6}}$.
(2)原式$=\frac {x(x+y)}{x(x-y)}\cdot \frac {1}{x+y}\cdot \frac {y(y-x)}{-xy}=\frac {1}{x}.$

15. 先化简：$\frac{a - 1}{a + 2} \cdot \frac{a - 4}{a^{3}-2a^{2}+a} ÷ \frac{2a + 2}{a^{2}-1}$，再用一个你喜欢且使分式有意义的数代替 $a$ 计算结果。

答案： 15.解:原式$=\frac {a-1}{a+2}\cdot \frac {(a+2)(a-2)}{a(a-1)^{2}}\cdot \frac {(a+1)(a-1)}{2(a+1)}=\frac {a-2}{2a}.\because a≠0$且$a≠\pm 1,\pm 2$,
∴a可以等于 3. 当$a=3$时,原式$=\frac {1}{6}$. (答案不唯一)

16. 如图，“丰收 1 号”小麦的试验田是边长为 $a$ m($a ＞ 1$)的正方形去掉一个边长为 $1$ m 的正方形蓄水池后余下的部分，“丰收 2 号”小麦的试验田是边长为 $(a - 1)$m 的正方形，两块试验田的小麦都收获了 $500$ kg。
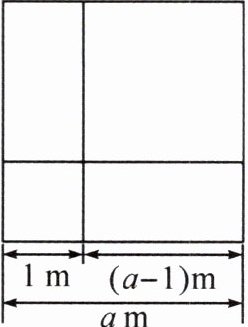
(1)“丰收2号”小麦的单位面积产量高。(填“丰收 1 号”或“丰收 2 号”)
(2)高的单位面积产量是低的单位面积产量的多少倍？

答案： 16.解:
(1)丰收2号
(2)$\because \frac {500}{a^{2}-1}＜\frac {500}{(a-1)^{2}},\therefore \frac {500}{(a-1)^{2}}÷\frac {500}{a^{2}-1}=$$\frac {500}{(a-1)^{2}}\cdot \frac {a^{2}-1}{500}=\frac {500}{(a-1)^{2}}\cdot \frac {(a-1)(a+1)}{500}=\frac {a+1}{a-1}$.
答:高的单位面积产量是低的单位面积产量的$\frac {a+1}{a-1}$倍.

【例】已知 $x + \frac{1}{x} = 3$，试求下列各式的值：
(1) $x^{2} + \frac{1}{x^{2}} =$7；(2) $x^{4} + \frac{1}{x^{4}} =$47；
(3) $x - \frac{1}{x} =$$\pm\sqrt{5}$。

答案： 【例】
(1)7
(2)47
(3)$\pm \sqrt {5}$

1. 已知 $x^{2}-3x + 1 = 0$，求 $x^{2} + \frac{1}{x^{2}}$ 的值。
2. 若 $x^{2}-4x - 1 = 0$，则 $\frac{3x^{2}}{x^{4}-7x^{2}+1} =$$\frac{3}{11}$。

答案： 1.解:$x^{2}-3x+1=0$移项,得$x^{2}+1=3x$. 两边同除以x,得$x+\frac {1}{x}=3.$$\therefore (x+\frac {1}{x})^{2}=3^{2}$,即$x^{2}+\frac {1}{x^{2}}+2=9.\therefore x^{2}+\frac {1}{x^{2}}=7.$ 2.$\frac {3}{11}$