《2025年名校课堂八年级数学上册冀教版河北专版》

12. 如图，若$a = 2b$，则表示$\frac{a^{2}-ab}{a^{2}-b^{2}}$的值的点落在(C)


A.第①段
B.第②段
C.第③段
D.第④段

答案： 12.C

13. 新考向 过程性学习 化简$\frac{16a^{2}-b^{2}}{4a + b}$时，小明、小华两位同学的化简过程如下：
小明：$\frac{16a^{2}-b^{2}}{4a + b}=\frac{(4a + b)(4a - b)}{4a + b}=4a - b$；
小华：$\frac{16a^{2}-b^{2}}{4a + b}=\frac{(16a^{2}-b^{2})(4a - b)}{(4a + b)(4a - b)}=4a - b$.
对于他俩的解法，你的看法是(B)

A.都正确
B.小明正确，小华不正确
C.小华正确，小明不正确
D.都不正确

答案： 13.B

14. (教材 P7 习题 T3 变式)如图，计算长方形$ABCD$与长方形$EFGH$的面积比.

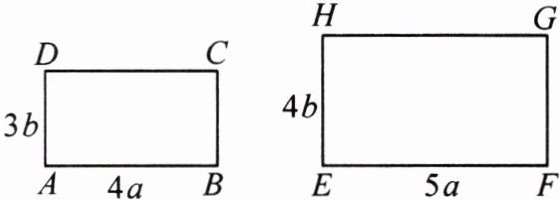
答案： 14.解:$\because S_{长方形ABCD}=4a\cdot 3b=12ab,S_{长方形EFGH}=5a\cdot 4b=20ab$,
∴长方形ABCD 与长方形 EFGH 的面积比为$\frac {12ab}{20ab}=\frac {3}{5}.$

15. 【整体思想】已知$x - y = xy$，求分式$\frac{3x - 5xy - 3y}{y - 2xy - x}$的值.

答案： 15.解:$\frac {3x-5xy-3y}{y-2xy-x}=\frac {3(x-y)-5xy}{-(x-y)-2xy}=\frac {3xy-5xy}{-xy-2xy}=\frac {-2xy}{-3xy}=\frac {2}{3}.$

16. 先化简，再求值：$\frac{8b^{2}-2a^{2}}{a^{2}-4ab + 4b^{2}}$，其中$a^{2}+10a + 25+\vert b - 4\vert = 0$.

答案： 16.解:原式$=\frac {2(4b^{2}-a^{2})}{(a-2b)^{2}}=\frac {2(2b+a)(2b-a)}{(a-2b)^{2}}=\frac {2(2b+a)}{2b-a}.\because a^{2}+10a+25+|b-4|=0,\therefore (a+5)^{2}+|b-4|=0.\therefore a+5=0,b-4=0.\therefore a=-5,b=4$.
∴原式$=\frac {2×(8-5)}{8+5}=\frac {6}{13}.$

17. 新考向 阅读理解 小学里，把分子比分母小的数叫作真分数.类似地，我们把分子的次数小于分母的次数的分式称为真分式，反之，称为假分式.对于任何一个假分式，都可以化成整式与真分式的和的形式.如：$\frac{x + 1}{x - 1}=\frac{x - 1 + 2}{x - 1}=\frac{x - 1}{x - 1}+\frac{2}{x - 1}=1+\frac{2}{x - 1}$.
(1)下列分式中，属于真分式的是(C)
A. $\frac{x^{2}}{x - 1}$
B. $\frac{x - 1}{x + 1}$
C. $-\frac{3}{2x - 1}$
D. $\frac{x^{2}+1}{x^{2}-1}$
(2)将假分式$\frac{m^{2}+3}{m + 1}$化成整式与真分式的和的形式.
(3)若$\frac{m^{2}+3}{m + 1}$的值是整数，求整数$m$的值.

答案： 17.解:
(1)C
(2)$\frac {m^{2}+3}{m+1}=\frac {m^{2}-1+4}{m+1}=\frac {m^{2}-1}{m+1}+\frac {4}{m+1}=m-1+\frac {4}{m+1}$.
(3)由
(2)得$\frac {m^{2}+3}{m+1}=m-1+\frac {4}{m+1}$.
∵$\frac {m^{2}+3}{m+1}$的值为整数,且 m 为整数,
∴$m+1=-1$或1或-4或4或-2或2.
∴$m=-2$或0或-5或3或-3或1.