第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. $2÷0.02=$
$8÷0.4=$
$3.5×0.6=$
$7.2÷9=$
$2.1 + 0.47=$
$\frac{7}{10}-\frac{1}{4}=$
$\frac{1}{2}+\frac{7}{20}=$
100
$0.15×8=$1.2
$0.2×0.6=$0.12
$8÷0.4=$
20
$1.8 - 0.08=$1.72
$3.2÷0.8=$4
$3.5×0.6=$
2.1
$5.2 + 0.25=$5.45
$2.6×50=$130
$7.2÷9=$
0.8
$1.6÷80=$0.02
$3.5 + 17.6=$21.1
$2.1 + 0.47=$
2.57
$0.35×0.2=$0.07
$4.2 - 0.58=$3.62
$\frac{7}{10}-\frac{1}{4}=$
$\frac{9}{20}$
$\frac{14}{15}-\frac{1}{3}=$$\frac{3}{5}$
$\frac{3}{2}+\frac{2}{15}=$$\frac{49}{30}$
$\frac{1}{2}+\frac{7}{20}=$
$\frac{17}{20}$
$\frac{13}{16}-\frac{1}{4}=$$\frac{9}{16}$
$5-\frac{5}{18}=$$4\frac{13}{18}$
答案:
1. 100 1.2 0.12
20 1.72 4
2.1 5.45 130
0.8 0.02 21.1
2.57 0.07 3.62
$\frac{9}{20}$ $\frac{3}{5}$ $\frac{49}{30}$
$\frac{17}{20}$ $\frac{9}{16}$ $4\frac{13}{18}$
20 1.72 4
2.1 5.45 130
0.8 0.02 21.1
2.57 0.07 3.62
$\frac{9}{20}$ $\frac{3}{5}$ $\frac{49}{30}$
$\frac{17}{20}$ $\frac{9}{16}$ $4\frac{13}{18}$
2. 计算下面各图形的表面积和体积。
(1)

(2)

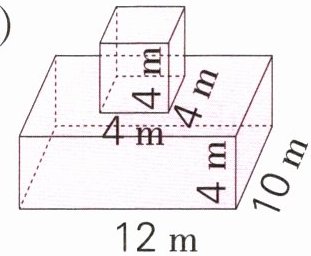
(3)
]
(1)

(2)

(3)
]

答案:
1. (1)
长方体表面积公式$S=(ab + ah+bh)×2$($a = 40m$,$b = 40m$,$h = 18m$),体积公式$V=abh$。
表面积:
$S=(40×40 + 40×18+40×18)×2$
$=(1600 + 720+720)×2$
$=(1600 + 1440)×2$
$=3040×2$
$=6080(m^{2})$
体积:
$V = 40×40×18$
$=1600×18$
$=28800(m^{3})$
2. (2)
正方体表面积公式$S = 6a^{2}$($a = 6dm$),体积公式$V=a^{3}$。
表面积:
$S=6×6×6$
$=36×6$
$=216(dm^{2})$
体积:
$V = 6×6×6$
$=216(dm^{3})$
3. (3)
表面积:
把组合体的表面积看作大长方体的表面积加上小长方体$4$个侧面的面积。
大长方体$a = 12m$,$b = 10m$,$h = 4m$,小长方体$a = 4m$,$b = 4m$,$h = 4m$。
大长方体表面积$S_{1}=(12×10 + 12×4+10×4)×2=(120 + 48 + 40)×2=(168 + 40)×2=208×2 = 416(m^{2})$。
小长方体$4$个侧面面积$S_{2}=4×4×4 = 64(m^{2})$。
组合体表面积$S=416+64=480(m^{2})$。
体积:
大长方体体积$V_{1}=12×10×4 = 480(m^{3})$,小长方体体积$V_{2}=4×4×4 = 64(m^{3})$。
组合体体积$V=V_{1}+V_{2}=480 + 64=544(m^{3})$。
综上,(1)表面积$6080m^{2}$,体积$28800m^{3}$;(2)表面积$216dm^{2}$,体积$216dm^{3}$;(3)表面积$480m^{2}$,体积$544m^{3}$。
长方体表面积公式$S=(ab + ah+bh)×2$($a = 40m$,$b = 40m$,$h = 18m$),体积公式$V=abh$。
表面积:
$S=(40×40 + 40×18+40×18)×2$
$=(1600 + 720+720)×2$
$=(1600 + 1440)×2$
$=3040×2$
$=6080(m^{2})$
体积:
$V = 40×40×18$
$=1600×18$
$=28800(m^{3})$
2. (2)
正方体表面积公式$S = 6a^{2}$($a = 6dm$),体积公式$V=a^{3}$。
表面积:
$S=6×6×6$
$=36×6$
$=216(dm^{2})$
体积:
$V = 6×6×6$
$=216(dm^{3})$
3. (3)
表面积:
把组合体的表面积看作大长方体的表面积加上小长方体$4$个侧面的面积。
大长方体$a = 12m$,$b = 10m$,$h = 4m$,小长方体$a = 4m$,$b = 4m$,$h = 4m$。
大长方体表面积$S_{1}=(12×10 + 12×4+10×4)×2=(120 + 48 + 40)×2=(168 + 40)×2=208×2 = 416(m^{2})$。
小长方体$4$个侧面面积$S_{2}=4×4×4 = 64(m^{2})$。
组合体表面积$S=416+64=480(m^{2})$。
体积:
大长方体体积$V_{1}=12×10×4 = 480(m^{3})$,小长方体体积$V_{2}=4×4×4 = 64(m^{3})$。
组合体体积$V=V_{1}+V_{2}=480 + 64=544(m^{3})$。
综上,(1)表面积$6080m^{2}$,体积$28800m^{3}$;(2)表面积$216dm^{2}$,体积$216dm^{3}$;(3)表面积$480m^{2}$,体积$544m^{3}$。
3. 一个长 $10dm$、宽 $3dm$ 的长方体玻璃缸,缸中有 $96L$ 水。把一块不规则的铁块放入水中(铁块完全浸没且水未溢出),这时水深 $4.8dm$。这块铁块的体积是多少立方分米?
答案:
3.$48\ \text{dm}^3$
查看更多完整答案,请扫码查看


