《2025年小学学霸天天计算六年级上册苏教版》

$1. 0.32÷4=0.08 0.06×0.5=0.03 0.84÷4=0.21 3.75×200=750 4.5+5.4=9.9 1.03-0.3=0.73 4.15+4.85=9 5.4÷18=0.3 750×0.4=300 \frac{2}{3}+\frac{1}{8}=$\frac{19}{24}$ \frac{5}{3}+\frac{1}{9}=$\frac{16}{9}$ \frac{3}{2}-\frac{7}{8}=$\frac{5}{8}$ \frac{5}{4}-\frac{5}{12}=$\frac{5}{6}$ \frac{7}{10}-\frac{2}{15}=$\frac{17}{30}$ \frac{1}{6}+\frac{1}{10}=$\frac{4}{15}$$

答案： 0.08 0.03 0.21 750 9.9 0.73 9 0.3 300 $\frac{19}{24}$ $\frac{16}{9}$ $\frac{5}{8}$ $\frac{5}{6}$ $\frac{17}{30}$ $\frac{4}{15}$

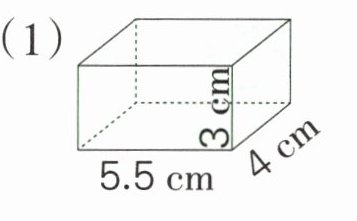
2. 计算下面长方体、正方体的底面积和体积。
(1)

(2)

答案： 1. 对于长方体：
长方体底面积公式$S = ab$（$a$为长，$b$为宽），体积公式$V=Sh$（$S$为底面积，$h$为高）。
底面积：
已知$a = 5.5cm$，$b = 4cm$，根据$S=ab$，可得$S = 5.5×4=22(cm^{2})$。
体积：
已知$S = 22cm^{2}$，$h = 3cm$，根据$V = Sh$，可得$V=22×3 = 66(cm^{3})$。
2. 对于正方体：
正方体底面积公式$S=a^{2}$（$a$为棱长），体积公式$V = a^{3}$（或$V=Sh$，此时$S=a^{2}$，$h = a$）。
底面积：
已知$a = 20m$，根据$S=a^{2}$，可得$S=20×20 = 400(m^{2})$。
体积：
已知$a = 20m$，根据$V=a^{3}$，可得$V=20×20×20=8000(m^{3})$。
综上，（1）长方体底面积为$22cm^{2}$，体积为$66cm^{3}$；（2）正方体底面积为$400m^{2}$，体积为$8000m^{3}$。

3. 王叔叔收藏了一方平板砚台,形状近似长方体。砚台的底面积是$138 cm^2,$高是2.5 cm。如果每立方厘米砚台约重2.2 g,这方平板砚台约重多少克?

答案： $759\ \text{g}$