2025年暑假训练营学年总复习八年级数学北师大版希望出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假训练营学年总复习八年级数学北师大版希望出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 如图,已知 BG 是∠ABC 的平分线,DE⊥AB 于点 E,DF⊥BC 于点 F,DE= 6,则 DF 的长度是(
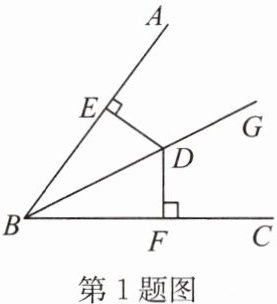
A.2
B.3
C.4
D.6
D
)
A.2
B.3
C.4
D.6
答案:
D
2. 如图,OC 为∠AOB 的平分线,CM⊥OB,OC= 5,OM= 4,则点 C 到射线 OA 的距离为______.
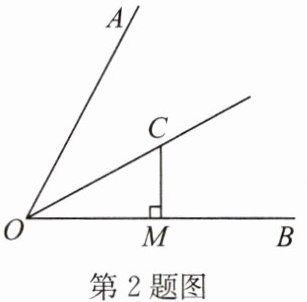
2. 如图,OC 为∠AOB 的平分线,CM⊥OB,OC= 5,OM= 4,则点 C 到射线 OA 的距离为

2. 如图,OC 为∠AOB 的平分线,CM⊥OB,OC= 5,OM= 4,则点 C 到射线 OA 的距离为
3
.
答案:
3
3. 如图,AB//CD,∠ABC 和∠DCB 的平分线 BP,CP 交于点 P,过点 P 作 PA⊥AB 于点 A,交 CD 于点 D. 若 AD= 10,则点 P 到 BC 的距离是
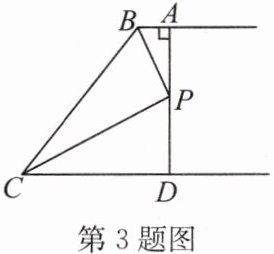
5
,∠BPC= $ 90 ^ { \circ } $
.
答案:
5 $ 90 ^ { \circ } $
4. 如图,△ABC 的周长是 32,OB,OC 分别平分∠ABC 和∠ACB,OD⊥BC 于点 D,且 OD= 6,则△ABC 的面积是______.
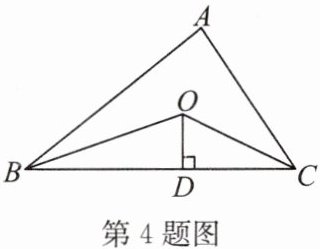
4. 如图,△ABC 的周长是 32,OB,OC 分别平分∠ABC 和∠ACB,OD⊥BC 于点 D,且 OD= 6,则△ABC 的面积是______.

4. 如图,△ABC 的周长是 32,OB,OC 分别平分∠ABC 和∠ACB,OD⊥BC 于点 D,且 OD= 6,则△ABC 的面积是

4. 如图,△ABC 的周长是 32,OB,OC 分别平分∠ABC 和∠ACB,OD⊥BC 于点 D,且 OD= 6,则△ABC 的面积是______.

4. 如图,△ABC 的周长是 32,OB,OC 分别平分∠ABC 和∠ACB,OD⊥BC 于点 D,且 OD= 6,则△ABC 的面积是
96
.
答案:
96
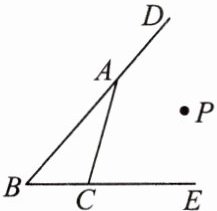
5. 如图,已知点 P 到 BE,BD,AC 的距离恰好相等,则点 P 的位置:①在∠B 的平分线上;②在∠DAC 的平分线上;③在∠ECA 的平分线上;④恰在∠B,∠DAC,∠ECA 的平分线的交点处. 上述结论中,正确的有(
A.1 个
B.2 个
C.3 个
D.4 个
D
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:
D
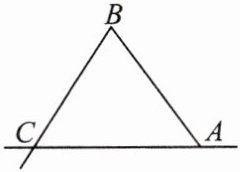
6. 现要在三角形地 ABC 内建一中心医院,使医院到 A,B 两个居民小区的距离相等,并且到公路 AB 和 AC 的距离也相等,请确定这个中心医院的位置.(保留作图痕迹)

答案:
解:作 AB 的垂直平分线 EF,作 $ \angle B A C $ 的平分线 AM,两线交于点 P,则点 P 为这个中心医院的位置.
解:作 AB 的垂直平分线 EF,作 $ \angle B A C $ 的平分线 AM,两线交于点 P,则点 P 为这个中心医院的位置.

7. 已知△ABC 内一点 P,如果点 P 到 AB,AC 两边的距离相等,则点 P(
A.在 B
B.在 B
C.在∠BA
D.在 B
C
)A.在 B
B.在 B
C.在∠BA
D.在 B
答案:
C
8. 如图,△ABC 的三边 AB,BC,CA 的长分别为 40,50,60,其三条角平分线交于点 O,则 $ S_{\triangle ABO}:S_{\triangle BCO}:S_{\triangle CAO} $ =
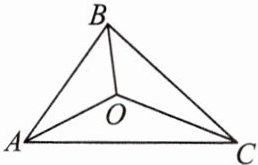
$ 4 : 5 : 6 $
.
答案:
$ 4 : 5 : 6 $
查看更多完整答案,请扫码查看


