2025年一本预备六年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一本预备六年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
例题:一个画框的尺寸如右图,做这个画框需要多长的木条?

[例题探究]
1. 理解题意。
根据右图可知,这个画框是一个长$\frac{4}{5}m$、宽$\frac{1}{2}m$的长方形,求做这个画框需要多长的木条,就是求这个长方形的周长。
2. 根据长方形的周长计算公式列式。
$(\frac{4}{5}+\frac{1}{2})× 2或\frac{4}{5}× 2+\frac{1}{2}× 2$
3. 明确运算顺序。
分数混合运算的运算顺序和整数混合运算的运算顺序相同。
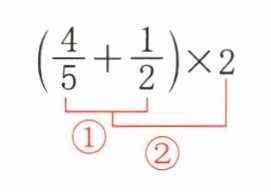

[规范解答]
方法一:$(\frac{4}{5}+\frac{1}{2})× 2= ( )(m)$ 方法二:$\frac{4}{5}× 2+\frac{1}{2}× 2= ( )(m)$
答:做这个画框需要( )m 长的木条。

[例题探究]
1. 理解题意。
根据右图可知,这个画框是一个长$\frac{4}{5}m$、宽$\frac{1}{2}m$的长方形,求做这个画框需要多长的木条,就是求这个长方形的周长。
2. 根据长方形的周长计算公式列式。
$(\frac{4}{5}+\frac{1}{2})× 2或\frac{4}{5}× 2+\frac{1}{2}× 2$
3. 明确运算顺序。
分数混合运算的运算顺序和整数混合运算的运算顺序相同。


[规范解答]
方法一:$(\frac{4}{5}+\frac{1}{2})× 2= ( )(m)$ 方法二:$\frac{4}{5}× 2+\frac{1}{2}× 2= ( )(m)$
答:做这个画框需要( )m 长的木条。
答案:
$\frac{13}{5}$ $\frac{13}{5}$ $\frac{13}{5}$
例题 1:计算下面每组的两个算式,看看它们有什么关系。
$\frac{1}{2}× \frac{1}{3}$
$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}$
$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}$
[例题探究]
1. 计算结果。
2. 发现规律。
$\frac{1}{2}× \frac{1}{3}= \frac{1}{3}× \frac{1}{2}$符合乘法交换律。
$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}= \frac{1}{4}× (\frac{2}{3}× \frac{3}{5})$符合乘法结合律。
$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}= \frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}$符合乘法分配律。
发现:
$\frac{1}{2}× \frac{1}{3}$
=
$\frac{1}{3}× \frac{1}{2}$$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}$
=
$\frac{1}{4}× (\frac{2}{3}× \frac{3}{5})$$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}$
=
$\frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}$[例题探究]
1. 计算结果。
$\frac{1}{2}× \frac{1}{3}=\frac{1}{6}$,$\frac{1}{3}× \frac{1}{2}=\frac{1}{6}$,$\frac{1}{2}× \frac{1}{3}=\frac{1}{3}× \frac{1}{2}$;
$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}=\frac{1}{6}×\frac{3}{5}=\frac{1}{10}$,$\frac{1}{4}× (\frac{2}{3}× \frac{3}{5})=\frac{1}{4}×\frac{2}{5}=\frac{1}{10}$,$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}=\frac{1}{4}× (\frac{2}{3}× \frac{3}{5})$;
$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}=\frac{5}{6}×\frac{1}{5}=\frac{1}{6}$,$\frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}=\frac{1}{10}+\frac{1}{15}=\frac{1}{6}$,$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}=\frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}$;
$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}=\frac{1}{6}×\frac{3}{5}=\frac{1}{10}$,$\frac{1}{4}× (\frac{2}{3}× \frac{3}{5})=\frac{1}{4}×\frac{2}{5}=\frac{1}{10}$,$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}=\frac{1}{4}× (\frac{2}{3}× \frac{3}{5})$;
$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}=\frac{5}{6}×\frac{1}{5}=\frac{1}{6}$,$\frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}=\frac{1}{10}+\frac{1}{15}=\frac{1}{6}$,$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}=\frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}$;
2. 发现规律。
$\frac{1}{2}× \frac{1}{3}= \frac{1}{3}× \frac{1}{2}$符合乘法交换律。
$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}= \frac{1}{4}× (\frac{2}{3}× \frac{3}{5})$符合乘法结合律。
$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}= \frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}$符合乘法分配律。
发现:
整数乘法的交换律、结合律和分配律,对于分数乘法也适用。
答案:
$\frac{1}{2}× \frac{1}{3}=\frac{1}{6}$,$\frac{1}{3}× \frac{1}{2}=\frac{1}{6}$,$\frac{1}{2}× \frac{1}{3}=\frac{1}{3}× \frac{1}{2}$;
$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}=\frac{1}{6}×\frac{3}{5}=\frac{1}{10}$,$\frac{1}{4}× (\frac{2}{3}× \frac{3}{5})=\frac{1}{4}×\frac{2}{5}=\frac{1}{10}$,$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}=\frac{1}{4}× (\frac{2}{3}× \frac{3}{5})$;
$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}=\frac{5}{6}×\frac{1}{5}=\frac{1}{6}$,$\frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}=\frac{1}{10}+\frac{1}{15}=\frac{1}{6}$,$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}=\frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}$;
整数乘法的交换律、结合律和分配律,对于分数乘法也适用。
$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}=\frac{1}{6}×\frac{3}{5}=\frac{1}{10}$,$\frac{1}{4}× (\frac{2}{3}× \frac{3}{5})=\frac{1}{4}×\frac{2}{5}=\frac{1}{10}$,$(\frac{1}{4}× \frac{2}{3})× \frac{3}{5}=\frac{1}{4}× (\frac{2}{3}× \frac{3}{5})$;
$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}=\frac{5}{6}×\frac{1}{5}=\frac{1}{6}$,$\frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}=\frac{1}{10}+\frac{1}{15}=\frac{1}{6}$,$(\frac{1}{2}+\frac{1}{3})× \frac{1}{5}=\frac{1}{2}× \frac{1}{5}+\frac{1}{3}× \frac{1}{5}$;
整数乘法的交换律、结合律和分配律,对于分数乘法也适用。
查看更多完整答案,请扫码查看


