第123页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
16. (本小题6分)
2024沈阳铁西区期中如图,某学校计划利用一片空地为学生建一个长方形车棚,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路(阴影部分),其余部分停放自行车,已知长方形车棚的宽为$x$m,长为$(\frac{3}{2}x + 1)$m,小路的宽为2m,求停放自行车的面积。

2024沈阳铁西区期中如图,某学校计划利用一片空地为学生建一个长方形车棚,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路(阴影部分),其余部分停放自行车,已知长方形车棚的宽为$x$m,长为$(\frac{3}{2}x + 1)$m,小路的宽为2m,求停放自行车的面积。

答案:
16.解:根据题意,得(x-2)($\frac{3}{2}$x+1-2×2)=($\frac{3}{2}$x²-6x+6)(m²).
答:停放自行车的面积为($\frac{3}{2}$x²-6x+6)m².
答:停放自行车的面积为($\frac{3}{2}$x²-6x+6)m².
17. (本小题8分)
在日历上,我们可以发现其中某些数之间满足一定的规律,图1是2024年3月的日历示意图,任意选择图中所示的方框,每个框四个角上的数交叉相乘后求和,再与中间的数的平方的2倍作差,例如:$3× 19 + 5× 17 - 2× 11^{2}= -100$,$14× 30 + 16× 28 - 2× 22^{2}= -100$,不难发现,结果都是$-100$。
(1)如图2,设日历中所示图形中间的数为$x$,则框中其余四个数从小到大依次可以表示为______,______,______,______;
(2)请用含$x$的式子表示发现的规律:______;
(3)利用整式的运算对(2)中的规律加以证明。


在日历上,我们可以发现其中某些数之间满足一定的规律,图1是2024年3月的日历示意图,任意选择图中所示的方框,每个框四个角上的数交叉相乘后求和,再与中间的数的平方的2倍作差,例如:$3× 19 + 5× 17 - 2× 11^{2}= -100$,$14× 30 + 16× 28 - 2× 22^{2}= -100$,不难发现,结果都是$-100$。
(1)如图2,设日历中所示图形中间的数为$x$,则框中其余四个数从小到大依次可以表示为______,______,______,______;
(2)请用含$x$的式子表示发现的规律:______;
(3)利用整式的运算对(2)中的规律加以证明。


答案:
17.解:
(1)x-8;x-6;x+6;x+8
(2)(x+8)(x-8)+(x-6)(x+6)-2x²=-100
(3)证明:左边=x²-64+x²-36-2x²=-100=右边.
∴结论成立.
(1)x-8;x-6;x+6;x+8
(2)(x+8)(x-8)+(x-6)(x+6)-2x²=-100
(3)证明:左边=x²-64+x²-36-2x²=-100=右边.
∴结论成立.
18. (本小题8分)
新考向·过程性学习【公式背景】
平方差公式可以利用图形来直观描述和解释。如图1,在边长为$a的大正方形中剪去一个边长为b的小正方形(a > b)$,若用两种不同的方法来表示阴影部分的面积,就能得到公式$(a + b)(a - b)= a^{2}-b^{2}$。
【公式形成】
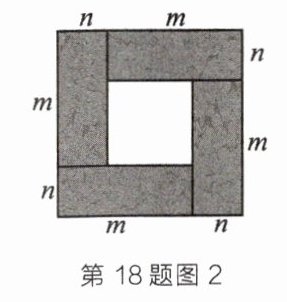
(1)如图2,用4张大小、形状相同的长方形纸片拼成一个大正方形,已知长方形的长、宽分别为$m$,$n(m > n)$,则$(m + n)^{2}$,$(m - n)^{2}和mn$之间的数量关系为______;
【公式应用】
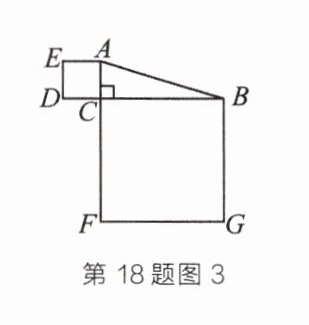
(2)如图3,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$BC > AC$。分别以$AC和BC$为边向外作两个正方形,已知$BD = 5$,$\triangle ABC$的面积是2,求$BC$的长。

新考向·过程性学习【公式背景】
平方差公式可以利用图形来直观描述和解释。如图1,在边长为$a的大正方形中剪去一个边长为b的小正方形(a > b)$,若用两种不同的方法来表示阴影部分的面积,就能得到公式$(a + b)(a - b)= a^{2}-b^{2}$。
【公式形成】
(1)如图2,用4张大小、形状相同的长方形纸片拼成一个大正方形,已知长方形的长、宽分别为$m$,$n(m > n)$,则$(m + n)^{2}$,$(m - n)^{2}和mn$之间的数量关系为______;
【公式应用】
(2)如图3,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$BC > AC$。分别以$AC和BC$为边向外作两个正方形,已知$BD = 5$,$\triangle ABC$的面积是2,求$BC$的长。



答案:
18.解:
(1)(m+n)²-(m-n)²=4mn
(2)
∵在Rt△ABC中,∠C=90°,
∴S△ABC=$\frac{1}{2}$BC·AC=2.
∴BC·AC=4.
∵BD=5,
∴BC+CD=BC+AC=5.
∴(BC-AC)²=(BC+AC)²-4BC·AC=25-16=9.
∵BC>AC,
∴BC-AC=3.
联立$\begin{cases} BC-AC=3, \\ BC+AC=5. \end{cases}$解得$\begin{cases} BC=4, \\ AC=1. \end{cases}$
∴BC的长为4.
(1)(m+n)²-(m-n)²=4mn
(2)
∵在Rt△ABC中,∠C=90°,
∴S△ABC=$\frac{1}{2}$BC·AC=2.
∴BC·AC=4.
∵BD=5,
∴BC+CD=BC+AC=5.
∴(BC-AC)²=(BC+AC)²-4BC·AC=25-16=9.
∵BC>AC,
∴BC-AC=3.
联立$\begin{cases} BC-AC=3, \\ BC+AC=5. \end{cases}$解得$\begin{cases} BC=4, \\ AC=1. \end{cases}$
∴BC的长为4.
19. (本小题12分)
2024沈阳期中新考向·新定义定义:如果$2^{m}= n(m$,$n$为正数),那么我们把$m叫作n的D$数,记作$m = D(n)$。
(1)根据$D$数的定义,填空:$D(2)= $______,$D(16)= $______;
(2)$D$数有如下运算性质:$D(st)= D(s)+D(t)$,$D(\frac{q}{p})= D(q)-D(p)$,其中$q > p$。
①若$D(a)= 1$,求$D(a^{3})$的值;
②若$D(3)= 2a - b$,$D(5)= a + c$,求$D(15)$,$D(\frac{5}{3})$,$D(108)$,$D(\frac{27}{20})$的值。(用含$a$,$b$,$c$的式子表示)
2024沈阳期中新考向·新定义定义:如果$2^{m}= n(m$,$n$为正数),那么我们把$m叫作n的D$数,记作$m = D(n)$。
(1)根据$D$数的定义,填空:$D(2)= $______,$D(16)= $______;
(2)$D$数有如下运算性质:$D(st)= D(s)+D(t)$,$D(\frac{q}{p})= D(q)-D(p)$,其中$q > p$。
①若$D(a)= 1$,求$D(a^{3})$的值;
②若$D(3)= 2a - b$,$D(5)= a + c$,求$D(15)$,$D(\frac{5}{3})$,$D(108)$,$D(\frac{27}{20})$的值。(用含$a$,$b$,$c$的式子表示)
答案:
19.解:
(1)1;4
解析
∵2¹=2,2⁴=16,
∴D
(2)=1,D
(16)=4.
(2)①
∵2¹=a,
∴a=2.
∴D(a³)=D(2³)=3.
②D
(15)=D(3×5)=D
(3)+D
(5)=(2a-b)+(a+c)=3a-b+c.
D($\frac{5}{3}$)=D
(5)-D
(3)=(a+c)-(2a-b)=-a+b+c.
D
(108)=D(3×3×3×2×2)=D
(3)+D
(3)+D
(3)+D
(2)+D
(2)=3×D
(3)+2×D
(2)=3×(2a-b)+2×1=6a-3b+2.
D($\frac{27}{20}$)=D
(27)-D
(20)=D(3×3×3)-D(5×2×2)=D
(3)+D
(3)+D
(3)-[D
(5)+D
(2)+D
(2)]=3×D
(3)-[D
(5)+2×D
(2)]=3×(2a-b)-(a+c+2×1)=6a-3b-a-c-2=5a-3b-c-2.
(1)1;4
解析
∵2¹=2,2⁴=16,
∴D
(2)=1,D
(16)=4.
(2)①
∵2¹=a,
∴a=2.
∴D(a³)=D(2³)=3.
②D
(15)=D(3×5)=D
(3)+D
(5)=(2a-b)+(a+c)=3a-b+c.
D($\frac{5}{3}$)=D
(5)-D
(3)=(a+c)-(2a-b)=-a+b+c.
D
(108)=D(3×3×3×2×2)=D
(3)+D
(3)+D
(3)+D
(2)+D
(2)=3×D
(3)+2×D
(2)=3×(2a-b)+2×1=6a-3b+2.
D($\frac{27}{20}$)=D
(27)-D
(20)=D(3×3×3)-D(5×2×2)=D
(3)+D
(3)+D
(3)-[D
(5)+D
(2)+D
(2)]=3×D
(3)-[D
(5)+2×D
(2)]=3×(2a-b)-(a+c+2×1)=6a-3b-a-c-2=5a-3b-c-2.
查看更多完整答案,请扫码查看


