例 请你计算前三个算式,再根据规律直接写出后三个算式的结果。
$2×5=$
$222×555=$
$22222×55555=$
思路分析
前三个算式的积分别为 10,1210,123210,从中可以发现,各个算式积的末尾比宝塔数(从高位到中间一位递增,从中间一位到 1 递减的数)多了一个 0。
解答:10 1210 123210 12343210 1234543210 123456543210
$2×5=$
10
$22×55=$1210
$222×555=$
123210
$2222×5555=$12343210
$22222×55555=$
1234543210
$222222×555555=$123456543210
思路分析
前三个算式的积分别为 10,1210,123210,从中可以发现,各个算式积的末尾比宝塔数(从高位到中间一位递增,从中间一位到 1 递减的数)多了一个 0。
解答:10 1210 123210 12343210 1234543210 123456543210
答案:
2×5=10
22×55=1210
222×555=123210
2222×5555=12343210
22222×55555=1234543210
222222×555555=123456543210
22×55=1210
222×555=123210
2222×5555=12343210
22222×55555=1234543210
222222×555555=123456543210
你知道其他几个算式的结果吗?
$37×3= 111$
$37×6= 222$
$37×9= 333$
$37×12= (
$37×15= (
$37×18= (
$37×3= 111$
$37×6= 222$
$37×9= 333$
$37×12= (
444
)$$37×15= (
555
)$$37×18= (
666
)$
答案:
444 555 666
例 如下图,这个算式的乘积是多少?
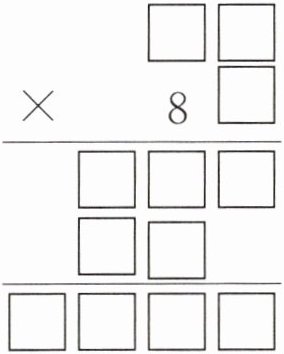

1068
答案:
1. 确定第一个乘数:第一个乘数为两位数,设为$AB$。因$AB×8$(第二个乘数十位数字8)的积是两位数,故$AB$可能为10、11、12。
2. 排除不可能值:若$AB=10$或11,$AB×C$($C$为第二个乘数个位数字)的积最大为$11×9=99$(两位数),不符合第一行部分积为三位数,排除。
3. 确定第一个乘数及第二个乘数个位:$AB=12$时,$12×C$需为三位数,则$C≥9$($C$为个位数),故$C=9$,第二个乘数为89。
4. 计算乘积:$12×89=1068$。
解答:$12×89 = 1068$
2. 排除不可能值:若$AB=10$或11,$AB×C$($C$为第二个乘数个位数字)的积最大为$11×9=99$(两位数),不符合第一行部分积为三位数,排除。
3. 确定第一个乘数及第二个乘数个位:$AB=12$时,$12×C$需为三位数,则$C≥9$($C$为个位数),故$C=9$,第二个乘数为89。
4. 计算乘积:$12×89=1068$。
解答:$12×89 = 1068$
已知 $□$ 里的数字都不是 1,完成下面竖式
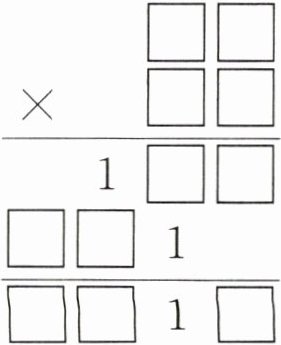

答案:
[附加题兴趣班]
$\begin{array}{r} \boxed{5}\ \boxed{3}\\ ×\ \boxed{7}\ \boxed{2}\\ \hline 1\ \boxed{0}\ \boxed{6}\\ \boxed{3}\ \boxed{7}\ 1\ \ \ \\ \hline \boxed{3}\ \boxed{8}\ 1\ \boxed{6}\end{array}$

[提示]将竖式中的几个位置上的数用字母表示,如图,由算式可知$e=0$,乘数$\overline{ab}$与$d$的乘积为$\overline{10f}$。由$c×\overline{ab}$的个位是1,得$c×\overline{ab}$是$7×\overline{a3}$或$3×\overline{a7}$或$9×\overline{a9}$。当$f=3,7,9$时,103,107,109都不能写成两位数与一位数相乘的形式;当$f=2$时,$102=17×6$,但$17×3$的积不是三位数,等式不成立;当$f=4$时,$104=13×8$,同样,$13×7$的积也不是三位数,等式不成立;当$f=6$时,$106=53×2$,而$53×7=371$,等式成立;当$f=8$时,$108=27×4$,$27×3$的积不是三位数,等式不成立。因此这个乘法算式是$53×72=3816$。
$\begin{array}{r} \boxed{a}\ \boxed{b}\\ ×\ \boxed{c}\ \boxed{d}\\ \hline 1\ \boxed{e}\ \boxed{f}\\ □\ □\ 1\ \ \ \\ \hline □\ □\ 1\ □\end{array}$

[附加题兴趣班]
$\begin{array}{r} \boxed{5}\ \boxed{3}\\ ×\ \boxed{7}\ \boxed{2}\\ \hline 1\ \boxed{0}\ \boxed{6}\\ \boxed{3}\ \boxed{7}\ 1\ \ \ \\ \hline \boxed{3}\ \boxed{8}\ 1\ \boxed{6}\end{array}$

[提示]将竖式中的几个位置上的数用字母表示,如图,由算式可知$e=0$,乘数$\overline{ab}$与$d$的乘积为$\overline{10f}$。由$c×\overline{ab}$的个位是1,得$c×\overline{ab}$是$7×\overline{a3}$或$3×\overline{a7}$或$9×\overline{a9}$。当$f=3,7,9$时,103,107,109都不能写成两位数与一位数相乘的形式;当$f=2$时,$102=17×6$,但$17×3$的积不是三位数,等式不成立;当$f=4$时,$104=13×8$,同样,$13×7$的积也不是三位数,等式不成立;当$f=6$时,$106=53×2$,而$53×7=371$,等式成立;当$f=8$时,$108=27×4$,$27×3$的积不是三位数,等式不成立。因此这个乘法算式是$53×72=3816$。
$\begin{array}{r} \boxed{a}\ \boxed{b}\\ ×\ \boxed{c}\ \boxed{d}\\ \hline 1\ \boxed{e}\ \boxed{f}\\ □\ □\ 1\ \ \ \\ \hline □\ □\ 1\ □\end{array}$

查看更多完整答案,请扫码查看


