例1
下面每个图中的$∠1与∠2$相等吗?说明理由。

下面每个图中的$∠1与∠2$相等吗?说明理由。

答案:
本题可通过分析图中$∠1$与$∠2$和中间夹角的关系来判断$∠1$与$∠2$是否相等。
左图:
$∠1$与中间夹角组成直角($90^{\circ}$),即$∠1 +$中间夹角$ = 90^{\circ}$;$∠2$与中间夹角也组成直角($90^{\circ}$),即$∠2 +$中间夹角$ = 90^{\circ}$。
所以$∠1 = 90^{\circ}-$中间夹角,$∠2 = 90^{\circ}-$中间夹角,由此可得$∠1 = ∠2$。
右图:
$∠1$与中间夹角组成平角($180^{\circ}$),即$∠1 +$中间夹角$ = 180^{\circ}$;$∠2$与中间夹角也组成平角($180^{\circ}$),即$∠2 +$中间夹角$ = 180^{\circ}$。
所以$∠1 = 180^{\circ}-$中间夹角,$∠2 = 180^{\circ}-$中间夹角,由此可得$∠1 = ∠2$。
综上,左图中$∠1$与$∠2$相等,因为它们分别与中间的夹角组成了一个直角;右图中$∠1$与$∠2$相等,因为它们分别与中间的夹角组成了一个平角。
左图:
$∠1$与中间夹角组成直角($90^{\circ}$),即$∠1 +$中间夹角$ = 90^{\circ}$;$∠2$与中间夹角也组成直角($90^{\circ}$),即$∠2 +$中间夹角$ = 90^{\circ}$。
所以$∠1 = 90^{\circ}-$中间夹角,$∠2 = 90^{\circ}-$中间夹角,由此可得$∠1 = ∠2$。
右图:
$∠1$与中间夹角组成平角($180^{\circ}$),即$∠1 +$中间夹角$ = 180^{\circ}$;$∠2$与中间夹角也组成平角($180^{\circ}$),即$∠2 +$中间夹角$ = 180^{\circ}$。
所以$∠1 = 180^{\circ}-$中间夹角,$∠2 = 180^{\circ}-$中间夹角,由此可得$∠1 = ∠2$。
综上,左图中$∠1$与$∠2$相等,因为它们分别与中间的夹角组成了一个直角;右图中$∠1$与$∠2$相等,因为它们分别与中间的夹角组成了一个平角。
1. 如右下图,两个长方形相交,$∠2$大小未知,$∠1和∠3$相等吗?请说明理由。


答案:
相等,理由如下:$∠1=90^{\circ }-∠2$
$∠3=90^{\circ }-∠2$
$∠1=∠3$
【提示】$∠1+∠2=90^{\circ },∠3+∠2=90^{\circ }$,因为$∠1$和$∠2$、$∠2$和$∠3$组成角的度数相同,所以$∠1=∠3$。
$∠3=90^{\circ }-∠2$
$∠1=∠3$
【提示】$∠1+∠2=90^{\circ },∠3+∠2=90^{\circ }$,因为$∠1$和$∠2$、$∠2$和$∠3$组成角的度数相同,所以$∠1=∠3$。
例2
如下图,将长方形纸折起来一个角,如果$∠1 = 25^{\circ}$,那么$∠2$的度数是多少?
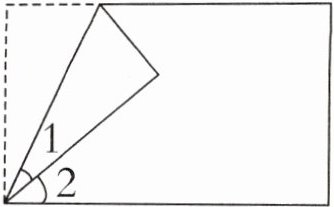
思路分析
$∠1翻折前的角与∠1$相等,且和$∠1以及∠2$构成一个直角,即$∠1 + ∠1 + ∠2 = 90^{\circ}$,又已知$∠1的度数为25^{\circ}$,则可求出$∠2$的度数。
解答
$∠2 = 90^{\circ} - ∠1 - ∠1 = 90^{\circ} - 25^{\circ} - 25^{\circ} = 40^{\circ}$
答:$∠2的度数是40^{\circ}$。
如下图,将长方形纸折起来一个角,如果$∠1 = 25^{\circ}$,那么$∠2$的度数是多少?

思路分析
$∠1翻折前的角与∠1$相等,且和$∠1以及∠2$构成一个直角,即$∠1 + ∠1 + ∠2 = 90^{\circ}$,又已知$∠1的度数为25^{\circ}$,则可求出$∠2$的度数。
解答
$∠2 = 90^{\circ} - ∠1 - ∠1 = 90^{\circ} - 25^{\circ} - 25^{\circ} = 40^{\circ}$
答:$∠2的度数是40^{\circ}$。
答案:
$∠2 = 90^{\circ} - 25^{\circ} × 2 = 40^{\circ}$。
答:$∠2$的度数是$40^{\circ}$。
答:$∠2$的度数是$40^{\circ}$。
2. 把长方形的纸如右下图折叠。已知$∠1 = 30^{\circ}$,则$∠2$,$∠3$各是多少度?
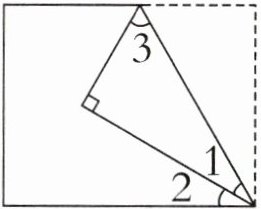

答案:
$∠2=90^{\circ }-∠1-∠1=30^{\circ }$
$∠3=180^{\circ }-90^{\circ }-∠1=60^{\circ }$
【提示】$∠1$与翻折前的角相等,因此$∠1+∠1+∠2=90^{\circ },∠2=30^{\circ }$;折叠起来的三角形是一个直角三角形,由此可知$∠3=180^{\circ }-90^{\circ }-30^{\circ }=60^{\circ }$。
$∠3=180^{\circ }-90^{\circ }-∠1=60^{\circ }$
【提示】$∠1$与翻折前的角相等,因此$∠1+∠1+∠2=90^{\circ },∠2=30^{\circ }$;折叠起来的三角形是一个直角三角形,由此可知$∠3=180^{\circ }-90^{\circ }-30^{\circ }=60^{\circ }$。
例3
如下图,已知$∠1 = 50^{\circ}$,求$∠4$的度数。

思路分析
找出图中4个角之间的关系是解题关键。从图中可知$∠1 + ∠2 = 90^{\circ}$,$∠2 + ∠3 = 90^{\circ}$,$∠3 + ∠4 = 90^{\circ}$,根据各角之间的关系,先求出$∠2$,再求出$∠3$,最后求出$∠4$;也可以先说明$∠1 = ∠3$,再求出$∠4$的度数。
解答
方法一:
$∠2 = 90^{\circ} - ∠1 = 90^{\circ} - 50^{\circ} = 40^{\circ}$
$∠3 = 90^{\circ} - ∠2 = 90^{\circ} - 40^{\circ} = 50^{\circ}$
$∠4 = 90^{\circ} - ∠3 = 90^{\circ} - 50^{\circ} = 40^{\circ}$
方法二:
$∠1 + ∠2 = 90^{\circ}$,$∠2 + ∠3 = 90^{\circ}$
$∠1 = ∠3 = 90^{\circ} - ∠2$,$∠1 = ∠3 = 50^{\circ}$
$∠4 = 90^{\circ} - ∠3 = 90^{\circ} - 50^{\circ} = 40^{\circ}$
答:$∠4的度数是40^{\circ}$。
如下图,已知$∠1 = 50^{\circ}$,求$∠4$的度数。

思路分析
找出图中4个角之间的关系是解题关键。从图中可知$∠1 + ∠2 = 90^{\circ}$,$∠2 + ∠3 = 90^{\circ}$,$∠3 + ∠4 = 90^{\circ}$,根据各角之间的关系,先求出$∠2$,再求出$∠3$,最后求出$∠4$;也可以先说明$∠1 = ∠3$,再求出$∠4$的度数。
解答
方法一:
$∠2 = 90^{\circ} - ∠1 = 90^{\circ} - 50^{\circ} = 40^{\circ}$
$∠3 = 90^{\circ} - ∠2 = 90^{\circ} - 40^{\circ} = 50^{\circ}$
$∠4 = 90^{\circ} - ∠3 = 90^{\circ} - 50^{\circ} = 40^{\circ}$
方法二:
$∠1 + ∠2 = 90^{\circ}$,$∠2 + ∠3 = 90^{\circ}$
$∠1 = ∠3 = 90^{\circ} - ∠2$,$∠1 = ∠3 = 50^{\circ}$
$∠4 = 90^{\circ} - ∠3 = 90^{\circ} - 50^{\circ} = 40^{\circ}$
答:$∠4的度数是40^{\circ}$。
答案:
方法一:
$∠2=90^{\circ}-∠1=90^{\circ}-50^{\circ}=40^{\circ}$
$∠3=90^{\circ}-∠2=90^{\circ}-40^{\circ}=50^{\circ}$
$∠4=90^{\circ}-∠3=90^{\circ}-50^{\circ}=40^{\circ}$
方法二:
因为$∠1+∠2=90^{\circ}$,$∠2+∠3=90^{\circ}$,所以$∠1=∠3=50^{\circ}$
$∠4=90^{\circ}-∠3=90^{\circ}-50^{\circ}=40^{\circ}$
答:$∠4$的度数是$40^{\circ}$。
$∠2=90^{\circ}-∠1=90^{\circ}-50^{\circ}=40^{\circ}$
$∠3=90^{\circ}-∠2=90^{\circ}-40^{\circ}=50^{\circ}$
$∠4=90^{\circ}-∠3=90^{\circ}-50^{\circ}=40^{\circ}$
方法二:
因为$∠1+∠2=90^{\circ}$,$∠2+∠3=90^{\circ}$,所以$∠1=∠3=50^{\circ}$
$∠4=90^{\circ}-∠3=90^{\circ}-50^{\circ}=40^{\circ}$
答:$∠4$的度数是$40^{\circ}$。
查看更多完整答案,请扫码查看


