《2025年实验班提优训练四年级数学上册北师大版》

例1(教材P9)
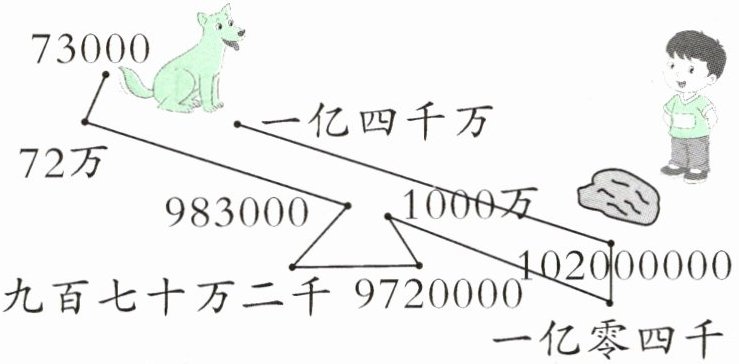
把下图中的点按数的大小从小到大连接起来。

思路分析
比较几个数的大小,先比较它们的位数,位数多的就大；位数相同的,从数的最高位开始比较,最高位上的数字大的那个数就大,最高位数字相同,就比较下一位,依次类推。
解答：

答案： 73000＜72万＜983000＜九百七十万二千＜9720000＜1000万＜一亿零四千＜102000000＜一亿四千万

比较数的大小时,不要只看数字的大小,一定要根据位数的多少和从高到低各级数位上的数字大小来进行判断。

答案： 假设要比较$A$和$B$两个数的大小（题目未给出具体数，以下为通用方法）。
若$A$位数比$B$位数多，则$A\gt B$；
若$A$位数比$B$位数少，则$A\lt B$；
若$A$和$B$位数相同，从最高位比起，最高位数字大的那个数大，如果最高位数字相同，就比较下一位，依次类推。
例如比较$3256$和$3218$，它们位数相同，千位都是$3$，百位都是$2$，十位$5\gt1$，所以$3256\gt3218$。

1. 在$◯$里填上“$＞$”“$＜$”或“$=$”。
$400000万◯$＞$4$亿
$245600$$◯$＜$246500$
$90283800$$◯$＜$90284000$
$124000$$◯$＞$12$万

答案： ＞ ＜ ＜ ＞【提示】比较两个数的大小，先看位数的多少，位数多的数大；位数相同，从最高位比起，最高位上数字大的数大，最高位数字相同，就比较下一位，依次类推。

例2(教材P15)
如果在一则报道中,有一个数据为“约$6$万”,实际数据可能是多少呢？画出它的范围。

答案：
思路分析
一个数的近似数是$6$万,这个数一定大于$5万且小于7$万。要使“$5□□□□$”省略“万”后面的尾数“五入”后是$6$万,最小是$55000$；要使“$6□□□□$”省略“万”后面的尾数“四舍”后是$6$万,最大是$64999$。
解答：

用“四舍五入”法取近似值,要满足“最大”的条件,应“四舍”；要满足“最小”的条件,应“五入”。

答案： 答题卡：
根据题意，在利用“四舍五入”法取近似值时：
为满足“最大”条件，应使需要保留的位数后的数字尽可能大但小于5，从而可以舍去，即采用“四舍”；
为满足“最小”条件，应使需要保留的位数后的数字为5或大于5，从而可以进位，即采用“五入”。

2. 如下图,被圈中的有很多数,这些数四舍五入到万位约是(6)万。

A.$8$
B.$7$
C.$6$
D.$5$

答案： C 【提示】这些数比 55000 大，比 65000 小，四舍五入到万位约是 6 万。