《2025年假日数学吉林出版集团股份有限公司七年级人教版》

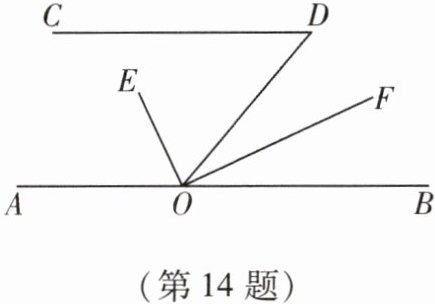
14. 已知,如图$CD// AB$,$OF平分∠BOD$,$OF⊥OE$,$∠D= 50^{\circ }$,求$∠DOE$的度数。

$∠DOE=$$65^{\circ }$.

答案： $\angle DOE = 65^{\circ}$.

15. (生活应用)老师为了让学生理解数学转化思想,设计了下面的问题：如图,有人想要测量两堵围墙在地面上所形成的$∠AOB$的度数,但人又不能进入围墙,只能站在围墙外。请问如何利用七年级所学习知识中“与角的数量关系有关的数学定理、基本事实等”设计测量方案？
方案1：学生甲说,我想到了对顶角相等。所以可以构造对顶角,如图,将测量$∠AOB转化为测量与∠AOB相等的对顶角∠COD$。
方案2：学生乙说：我想到了邻补角互补。所以可以构造邻补角,如图,将测量$∠AOB转化为测量与∠AOB互补的邻补角∠AOC或者∠BOD$。
方案3：学生丙说：我想到了平行线的性质定理,可以将需要测量的$∠AOB转化为与∠AOB$有着确定数量关系的其他角,例如内错角、同位角、同旁内角。
请你画出适当的示意图,选择恰当的平行线的性质,详细说明方案3的解决办法。
过点$O$作直线$EF// AB$（$AB$为$∠AOB$一边的延伸线），延长$BO$到$M$，测量$∠FOM$，由两直线平行，同位角相等，得$∠AOB = ∠FOM$（答案不唯一，也可根据内错角相等或同旁内角互补设计，只要符合平行线性质定理即可）

答案： 【解析】：
1. 首先，根据平行线的性质定理（两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补）来设计方案。
过点$O$作直线$EF// AB$（这里$AB$可看作是$∠AOB$的一条边的延伸线）。
然后在围墙外，延长$BO$（或$AO$），假设延长$BO$到点$M$。
因为$EF// AB$，根据两直线平行，同位角相等。如果我们测量出$∠FOM$（$∠FOM$与$∠AOB$是同位角）的度数，那么$∠AOB = ∠FOM$。
或者根据两直线平行，内错角相等。延长$AO$到点$N$，过点$O$作$PQ// BO$，测量$∠QON$（$∠QON$与$∠AOB$是内错角），则$∠AOB = ∠QON$。
又或者根据两直线平行，同旁内角互补。过点$O$作$GH// BO$，延长$AO$到点$K$，测量$∠GOK$，因为$∠AOB+∠GOK = 180^{\circ}$，所以$∠AOB=180^{\circ}-∠GOK$。
【答案】：
过点$O$作直线$EF// AB$（$AB$为$∠AOB$一边的延伸线），延长$BO$到$M$，测量$∠FOM$，由两直线平行，同位角相等，得$∠AOB = ∠FOM$（答案不唯一，也可根据内错角相等或同旁内角互补设计，只要符合平行线性质定理即可）。