2025年云南省标准教辅暑假活动五年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年云南省标准教辅暑假活动五年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 一个数的最大因数和最小倍数都是18,这个数是( ),它有( )个因数,有( )个倍数。
答案:
18,6,无数
2. 至少要用( )个完全相同的小正方体才能拼成一个大正方体。
答案:
$8$
3. 在括号里填上适当的分数。
75分=( )小时
45秒=( )分
75分=( )小时
45秒=( )分
答案:
$\frac{5}{4}$;$\frac{3}{4}$
4. 把10块糖平均分给5个小朋友,每个小朋友分得这些糖的$\frac{()}{()}$,3个小朋友分得这些糖的$\frac{()}{()}$,这个分数的分数单位是$\frac{()}{()}$,单位“1”是( )。
答案:
$\frac{1}{5}$,$\frac{3}{5}$,$\frac{1}{5}$,$10$块糖
5. 一个正方体的棱长总和是60cm,它的棱长是( ),体积是( ),表面积是( )。
答案:
5cm,125cm³,150cm²
1. 递等式计算。
$\frac{5}{8}-\frac{1}{4}+\frac{2}{3}$
$\frac{17}{8}-(\frac{1}{8}+\frac{2}{3})$
$2+\frac{15}{19}+\frac{4}{19}$
$\frac{5}{8}-\frac{1}{4}+\frac{2}{3}$
$\frac{17}{8}-(\frac{1}{8}+\frac{2}{3})$
$2+\frac{15}{19}+\frac{4}{19}$
答案:
【解析】:
对于$\frac{5}{8}-\frac{1}{4}+\frac{2}{3}$,先将$\frac{1}{4}$化为分母是$8$的分数$\frac{2}{8}$,则$\frac{5}{8}-\frac{2}{8}+\frac{2}{3}=\frac{3}{8}+\frac{2}{3}$,再通分,$8$和$3$的最小公倍数是$24$,$\frac{3}{8}=\frac{3\times3}{8\times3}=\frac{9}{24}$,$\frac{2}{3}=\frac{2\times8}{3\times8}=\frac{16}{24}$,所以$\frac{3}{8}+\frac{2}{3}=\frac{9}{24}+\frac{16}{24}=\frac{25}{24}$。
对于$\frac{17}{8}-(\frac{1}{8}+\frac{2}{3})$,根据去括号法则$a-(b + c)=a - b - c$,可得$\frac{17}{8}-\frac{1}{8}-\frac{2}{3}=\frac{16}{8}-\frac{2}{3}=2-\frac{2}{3}$,把$2$化为$\frac{6}{3}$,则$2-\frac{2}{3}=\frac{6}{3}-\frac{2}{3}=\frac{4}{3}$。
对于$2+\frac{15}{19}+\frac{4}{19}$,根据加法结合律$a + b + c=a+(b + c)$,可得$2+(\frac{15}{19}+\frac{4}{19})=2 + 1=3$。
【答案】:$\frac{25}{24}$;$\frac{4}{3}$;$3$
对于$\frac{5}{8}-\frac{1}{4}+\frac{2}{3}$,先将$\frac{1}{4}$化为分母是$8$的分数$\frac{2}{8}$,则$\frac{5}{8}-\frac{2}{8}+\frac{2}{3}=\frac{3}{8}+\frac{2}{3}$,再通分,$8$和$3$的最小公倍数是$24$,$\frac{3}{8}=\frac{3\times3}{8\times3}=\frac{9}{24}$,$\frac{2}{3}=\frac{2\times8}{3\times8}=\frac{16}{24}$,所以$\frac{3}{8}+\frac{2}{3}=\frac{9}{24}+\frac{16}{24}=\frac{25}{24}$。
对于$\frac{17}{8}-(\frac{1}{8}+\frac{2}{3})$,根据去括号法则$a-(b + c)=a - b - c$,可得$\frac{17}{8}-\frac{1}{8}-\frac{2}{3}=\frac{16}{8}-\frac{2}{3}=2-\frac{2}{3}$,把$2$化为$\frac{6}{3}$,则$2-\frac{2}{3}=\frac{6}{3}-\frac{2}{3}=\frac{4}{3}$。
对于$2+\frac{15}{19}+\frac{4}{19}$,根据加法结合律$a + b + c=a+(b + c)$,可得$2+(\frac{15}{19}+\frac{4}{19})=2 + 1=3$。
【答案】:$\frac{25}{24}$;$\frac{4}{3}$;$3$
2. 解方程。
$x-0.6x=24$ $x+\frac{5}{12}=\frac{13}{24}$
$x-0.6x=24$ $x+\frac{5}{12}=\frac{13}{24}$
答案:
【解析】:
对于方程$x - 0.6x = 24$,先对左边进行合并同类项,$x-0.6x=(1 - 0.6)x = 0.4x$,则原方程变为$0.4x = 24$,两边同时除以$0.4$,即$x=24\div0.4 = 60$。
对于方程$x+\frac{5}{12}=\frac{13}{24}$,根据等式的性质,等式两边同时减去$\frac{5}{12}$,则$x=\frac{13}{24}-\frac{5}{12}$,将$\frac{5}{12}$通分变为$\frac{10}{24}$,所以$x=\frac{13}{24}-\frac{10}{24}=\frac{3}{24}=\frac{1}{8}$。
【答案】:$x = 60$;$x=\frac{1}{8}$
对于方程$x - 0.6x = 24$,先对左边进行合并同类项,$x-0.6x=(1 - 0.6)x = 0.4x$,则原方程变为$0.4x = 24$,两边同时除以$0.4$,即$x=24\div0.4 = 60$。
对于方程$x+\frac{5}{12}=\frac{13}{24}$,根据等式的性质,等式两边同时减去$\frac{5}{12}$,则$x=\frac{13}{24}-\frac{5}{12}$,将$\frac{5}{12}$通分变为$\frac{10}{24}$,所以$x=\frac{13}{24}-\frac{10}{24}=\frac{3}{24}=\frac{1}{8}$。
【答案】:$x = 60$;$x=\frac{1}{8}$
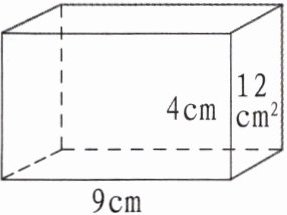
4. 求长方体的表面积和体积。

答案:
【解析】:
首先求长方体的宽,已知右侧面面积是$12cm^{2}$,高是$4cm$,根据长方形面积公式$S = a\times b$(这里右侧面$S =宽\times高$),可得宽$b=\frac{S}{高}=\frac{12}{4}=3cm$。
然后求长方体表面积$S_{表}$,根据长方体表面积公式$S_{表}=(ab + ah+bh)\times2$(其中$a = 9cm$,$b = 3cm$,$h = 4cm$),则$S_{表}=(9\times3 + 9\times4+3\times4)\times2=(27 + 36 + 12)\times2=(63 + 12)\times2=75\times2 = 150cm^{2}$。
再求长方体体积$V$,根据长方体体积公式$V=abh$,则$V=9\times3\times4 = 108cm^{3}$。
【答案】:表面积$150cm^{2}$,体积$108cm^{3}$。
首先求长方体的宽,已知右侧面面积是$12cm^{2}$,高是$4cm$,根据长方形面积公式$S = a\times b$(这里右侧面$S =宽\times高$),可得宽$b=\frac{S}{高}=\frac{12}{4}=3cm$。
然后求长方体表面积$S_{表}$,根据长方体表面积公式$S_{表}=(ab + ah+bh)\times2$(其中$a = 9cm$,$b = 3cm$,$h = 4cm$),则$S_{表}=(9\times3 + 9\times4+3\times4)\times2=(27 + 36 + 12)\times2=(63 + 12)\times2=75\times2 = 150cm^{2}$。
再求长方体体积$V$,根据长方体体积公式$V=abh$,则$V=9\times3\times4 = 108cm^{3}$。
【答案】:表面积$150cm^{2}$,体积$108cm^{3}$。
考考你
有9盒维生素E胶囊,其中一盒少了1粒,设法找出来,并试着用语言描述。

有9盒维生素E胶囊,其中一盒少了1粒,设法找出来,并试着用语言描述。

答案:
【解析】:将$9$盒维生素$E$胶囊分成$3$份,每份$3$盒。第一次,把其中两份分别放在天平秤两端,若天平秤平衡,则少$1$粒的那盒在未取的那份中;若不平衡,则少$1$粒的那盒在天平秤较轻一端的那份中。第二次,把有少$1$粒那盒的那份,任取$2$盒分别放在天平秤两端,若天平秤平衡,则未取那盒即为少$1$粒的;若不平衡,较轻一端的那盒即为少$1$粒的。
【答案】:将$9$盒分$3$份($3$,$3$,$3$),先称两份,再根据情况称其中$2$盒找出少$1$粒的那盒。
【答案】:将$9$盒分$3$份($3$,$3$,$3$),先称两份,再根据情况称其中$2$盒找出少$1$粒的那盒。
查看更多完整答案,请扫码查看


