《2025年云南省标准教辅暑假活动五年级数学人教版》

1. 按要求写数。
(1) 既是 2、5 的倍数，又是 3 的倍数的最小三位数是 ( )，最大三位数是 ( )。
(2) 既是 2 的倍数，又是 3 的倍数的最小三位数是 ( )，最大三位数是 ( )。

答案：
(1) 120，990；
(2) 102，996

2. 把下面每个图形都看作单位 “1”，用分数表示各图中的涂色部分。

( ) ( )

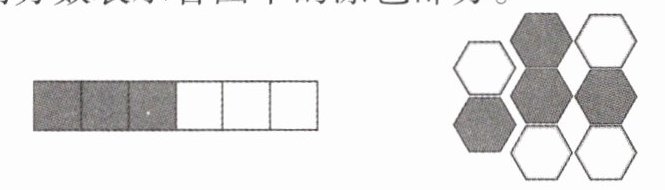
答案： $\frac{3}{6}$，$\frac{5}{3}$。

3. $\frac{5}{8}t$ 可以表示 ( ) t 的 $\frac{5}{8}$，也可以表示 ( ) t 的 $\frac{1}{8}$。

答案： 1；5

4. 一个数加上它的一个分数单位是 1，减去它的一个分数单位是 $\frac{8}{9}$，这个数是 ( )。

答案： $\frac{17}{18}$

1. 在 $\bigcirc$ 里填上 “＞” “＜” 或 “=”。$(a,b$ 不为 0)
$\frac{7}{11}+\frac{2}{9}\bigcirc\frac{2}{9}+\frac{7}{11}$ $a+\frac{7}{13}\bigcirc a+\frac{7}{15}$ $b-\frac{17}{19}\bigcirc b-\frac{2}{19}$

答案： 【解析】：
对于$\frac{7}{11}+\frac{2}{9}$和$\frac{2}{9}+\frac{7}{11}$，根据加法交换律，两个数相加，交换加数的位置，和不变，所以$\frac{7}{11}+\frac{2}{9}=\frac{2}{9}+\frac{7}{11}$。
对于$a+\frac{7}{13}$和$a+\frac{7}{15}$，因为$a$是相同的数，而$\frac{7}{13}$和$\frac{7}{15}$分子相同，分母越大分数越小，即$\frac{7}{13}＞\frac{7}{15}$，那么在$a$相同的情况下，加上一个较大的数结果更大，所以$a + \frac{7}{13}＞a+\frac{7}{15}$。
对于$b-\frac{17}{19}$和$b-\frac{2}{19}$，因为$b$是相同的数，$\frac{17}{19}＞\frac{2}{19}$，被减数相同，减数越大差越小，所以$b-\frac{17}{19}＜b - \frac{2}{19}$。
【答案】：=，＞，＜

2. 递等式计算。
$10-(\frac{1}{2}+0.4)$ $\frac{7}{6}+(\frac{3}{4}-\frac{5}{6})$

答案： 【解析】：
对于$10 - (\frac{1}{2}+0.4)$：
先将$\frac{1}{2}$化为小数，$\frac{1}{2}=0.5$。
再计算括号内的值：$0.5 + 0.4 = 0.9$。
最后计算括号外的值：$10 - 0.9 = 9.1$。
对于$\frac{7}{6}+(\frac{3}{4}-\frac{5}{6})$：
先去括号，$\frac{7}{6}+(\frac{3}{4}-\frac{5}{6})=\frac{7}{6}+\frac{3}{4}-\frac{5}{6}$。
利用加法交换律，$\frac{7}{6}+\frac{3}{4}-\frac{5}{6}=\frac{7}{6}-\frac{5}{6}+\frac{3}{4}$。
计算$\frac{7}{6}-\frac{5}{6}=\frac{2}{6}=\frac{1}{3}$。
再将$\frac{1}{3}$和$\frac{3}{4}$通分，$\frac{1}{3}=\frac{4}{12}$，$\frac{3}{4}=\frac{9}{12}$。
最后计算$\frac{4}{12}+\frac{9}{12}=\frac{13}{12}$。
【答案】：$9.1$；$\frac{13}{12}$

3. 解方程。
$\frac{7}{8}+x=\frac{23}{24}$ $\frac{2}{7}+\frac{13}{21}-x=\frac{3}{14}$

答案： 【解析】：
1. 对于方程$\frac{7}{8}+x = \frac{23}{24}$：
根据等式的性质，等式两边同时减去一个数，等式仍然成立。为了求出$x$的值，在方程两边同时减去$\frac{7}{8}$，则$x=\frac{23}{24}-\frac{7}{8}$。
先对$\frac{7}{8}$进行通分，$\frac{7}{8}=\frac{7\times3}{8\times3}=\frac{21}{24}$。
所以$x = \frac{23}{24}-\frac{21}{24}=\frac{23 - 21}{24}=\frac{2}{24}=\frac{1}{12}$。
2. 对于方程$\frac{2}{7}+\frac{13}{21}-x=\frac{3}{14}$：
先计算$\frac{2}{7}+\frac{13}{21}$，对$\frac{2}{7}$通分，$\frac{2}{7}=\frac{2\times3}{7\times3}=\frac{6}{21}$，则$\frac{2}{7}+\frac{13}{21}=\frac{6}{21}+\frac{13}{21}=\frac{6 + 13}{21}=\frac{19}{21}$，原方程变为$\frac{19}{21}-x=\frac{3}{14}$。
根据等式的性质，在等式两边同时加上$x$，得到$\frac{19}{21}=\frac{3}{14}+x$。
再在等式两边同时减去$\frac{3}{14}$，则$x=\frac{19}{21}-\frac{3}{14}$。
对$\frac{19}{21}$和$\frac{3}{14}$通分，$\frac{19}{21}=\frac{19\times2}{21\times2}=\frac{38}{42}$，$\frac{3}{14}=\frac{3\times3}{14\times3}=\frac{9}{42}$。
所以$x=\frac{38}{42}-\frac{9}{42}=\frac{38 - 9}{42}=\frac{29}{42}$。
【答案】：$x=\frac{1}{12}$；$x=\frac{29}{42}$

把下面的分数约分，是假分数的化成带分数或整数。
$\frac{108}{72}=$ $\frac{135}{90}=$
$\frac{14}{38}=$ $\frac{90}{18}=$

答案： 【解析】：
- 对于$\frac{108}{72}$，先求$108$和$72$的最大公因数，$108 = 2\times2\times3\times3\times3$，$72=2\times2\times2\times3\times3$，它们的最大公因数是$2\times2\times3\times3 = 36$，则$\frac{108\div36}{72\div36}=\frac{3}{2}=1\frac{1}{2}$。
- 对于$\frac{135}{90}$，$135 = 3\times3\times3\times5$，$90 = 2\times3\times3\times5$，最大公因数是$3\times3\times5 = 45$，所以$\frac{135\div45}{90\div45}=\frac{3}{2}=1\frac{1}{2}$。
- 对于$\frac{14}{38}$，$14 = 2\times7$，$38 = 2\times19$，最大公因数是$2$，那么$\frac{14\div2}{38\div2}=\frac{7}{19}$。
- 对于$\frac{90}{18}$，$90 = 2\times3\times3\times5$，$18 = 2\times3\times3$，最大公因数是$18$，故$\frac{90\div18}{18\div18}=5$。
【答案】：$1\frac{1}{2}$；$1\frac{1}{2}$；$\frac{7}{19}$；$5$

考考你 四个小朋友的年龄一个比一个大一岁，他们的年龄的乘积是 7920，四人当中，年龄最小的是几岁？

答案： 【解析】：
先把$7920$分解质因数：$7920 = 2\times2\times2\times2\times3\times3\times5\times11$。
然后将这些质因数凑成四个连续的自然数相乘的形式：$8\times9\times10\times11=(2\times2\times2)\times(3\times3)\times(2\times5)\times11 = 7920$。
【答案】：$8$