《2025年云南省标准教辅暑假活动五年级数学人教版》

1. 有三个连续的偶数，如果中间一个是 $ a $，那么另外两个是（ ）。
A. $ 2a $ 和 $ 4a $
B. $ a - 1 $ 和 $ a + 1 $
C. $ a - 2 $ 和 $ a + 2 $

答案： C

2. 从 1 里面连续减去（ ）个 $ \frac{1}{4} $，结果等于 $ \frac{1}{4} $。
A. $ \frac{1}{4} $
B. 1
C. 3
D. 4

答案： C

3. $ \frac{a}{11} + \frac{b}{11} $ 的结果是（ ）。
A. $ \frac{a + b}{22} $
B. $ \frac{ab}{11} $
C. $ \frac{a + b}{11} $
D. $ \frac{ab}{22} $

答案： C

1. 从 8 里面减去 $ \frac{3}{4} $ 与 1.6 的和，差是多少？

答案： 【解析】：本题可先求出$\frac{3}{4}$与$1.6$的和，再用$8$减去这个和，即可求出差。$\frac{3}{4}=0.75$，$\frac{3}{4}$与$1.6$的和为$0.75 + 1.6 = 2.35$，那么$8$减去它们的和的差是$8 - 2.35 = 5.65$。
【答案】：$5.65$

2. $ \frac{8}{9} $ 与 $ \frac{1}{3} $ 的差比 $ \frac{1}{6} $ 多多少？

答案： 【解析】：首先，计算$\frac{8}{9}$与$\frac{1}{3}$的差，即$\frac{8}{9}-\frac{1}{3}=\frac{8}{9}-\frac{3}{9}=\frac{5}{9}$；然后，求这个差比$\frac{1}{6}$多多少，用减法计算，$\frac{5}{9}-\frac{1}{6}=\frac{10}{18}-\frac{3}{18}=\frac{7}{18}$。
【答案】：$\frac{7}{18}$

有 248 个外形一样的小球，其中有一个较轻，如何用天平把这个较轻的球找出来？最少称几次？

答案： 【解析】：
本题可根据找次品问题的最优策略，将物品尽量平均分成$3$份来进行分析。
把$248$个球尽量平均分成$3$份，$248\div3 = 82\cdots\cdots2$，分成$82$、$82$、$84$。
第一次称：把两份$82$个的分别放在天平秤两端，如果天平平衡，则较轻的球在$84$个的那一份中；如果天平不平衡，则较轻的球在天平轻的一端的$82$个中。
情况一：若较轻的球在$84$个那一份中
把$84$个球平均分成$3$份，$84\div3 = 28$。
第二次称：把其中两份$28$个的分别放在天平秤两端，如果天平平衡，则较轻的球在没称的$28$个中；如果天平不平衡，则较轻的球在天平轻的一端的$28$个中。
把$28$个球平均分成$3$份，$28\div3 = 9\cdots\cdots1$，分成$9$、$9$、$10$。
第三次称：把两份$9$个的分别放在天平秤两端，如果天平平衡，则较轻的球在$10$个的那一份中；如果天平不平衡，则较轻的球在天平轻的一端的$9$个中。
若在$9$个球中，把$9$个球平均分成$3$份，$9\div3 = 3$。
第四次称：把其中两份$3$个的分别放在天平秤两端，如果天平平衡，则较轻的球在没称的$3$个中；如果天平不平衡，则较轻的球在天平轻的一端的$3$个中。
把$3$个球中的任意$2$个，分别放在天平秤两端。
第五次称：如果天平平衡，则没称的那个就是较轻的球；如果天平不平衡，轻的一端就是较轻的球。
若在$10$个球中，把$10$个球分成$3$、$3$、$4$。
第四次称：把两份$3$个的分别放在天平秤两端，如果天平平衡，则较轻的球在$4$个的那一份中；如果天平不平衡，则较轻的球在天平轻的一端的$3$个中。
若在$3$个球中，同上面称$3$个球的方法，再称一次可找出较轻的球；若在$4$个球中，把$4$个球分成$2$、$2$。
第五次称：把两份$2$个的分别放在天平秤两端，较轻的球在天平轻的一端的$2$个中。
第六次称：把这$2$个球分别放在天平秤两端，轻的一端就是较轻的球。
情况二：若较轻的球在$82$个那一份中
把$82$个球平均分成$3$份，$82\div3 = 27\cdots\cdots1$，分成$27$、$27$、$28$。
后续的称法与情况一中类似，也最多需要$6$次能找出较轻的球。
【答案】：把$248$个球尽量平均分成$3$份来称，最少称$6$次可以把较轻的球找出来。

1. 某粮店原有大米 $ \frac{7}{8}t $，卖出 $ \frac{3}{4}t $，又运来 $ \frac{1}{6}t $，粮店现有大米多少吨？

答案： 【解析】：首先，用原有的大米吨数减去卖出的吨数，可得到卖出后剩余的大米吨数，即$\frac{7}{8}-\frac{3}{4}$。通分计算$\frac{7}{8}-\frac{3}{4}=\frac{7}{8}-\frac{6}{8}=\frac{1}{8}$（吨）。然后，再用剩余的吨数加上又运来的吨数，就是粮店现有的大米吨数，即$\frac{1}{8}+\frac{1}{6}$。通分计算$\frac{1}{8}+\frac{1}{6}=\frac{3}{24}+\frac{4}{24}=\frac{7}{24}$（吨）。
【答案】：$\frac{7}{24}$

2. 小明比小丽小 12 岁，他们今年的年龄之和是 26 岁，且他们今年的年龄刚好都是质数。你知道小丽和小明今年分别有几岁吗？

答案： 【解析】：设小明今年$x$岁，因为小明比小丽小$12$岁，所以小丽今年$(x + 12)$岁。已知他们今年年龄之和是$26$岁，则可列方程$x+(x + 12)=26$，解方程$2x+12 = 26$，$2x=26 - 12$，$2x=14$，得$x = 7$。那么小丽的年龄是$x + 12=7 + 12 = 19$岁。再判断$7$和$19$是否为质数，质数是指在大于$1$的自然数中，除了$1$和它本身以外不再有其他因数的自然数，$7$的因数只有$1$和$7$，$19$的因数只有$1$和$19$，所以$7$和$19$都是质数，符合题意。
【答案】：小丽$19$岁，小明$7$岁

2. 如图，一个棱长为 8cm 的正方体，在它的一个角上挖掉一个棱长是 3cm 的小正方体，剩余部分的表面积是多少平方厘米？

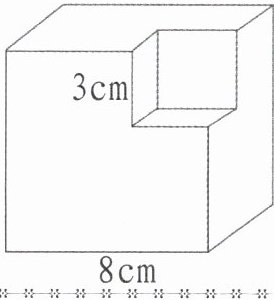
答案： 【解析】：本题可根据正方体的表面积公式，结合挖掉小正方体后表面积的变化情况来求解。
- **步骤一：分析挖掉小正方体后表面积的变化情况**
在大正方体的一个角上挖掉一个小正方体，原来大正方体表面减少了$3$个小正方形的面积，但是同时又增加了$3$个小正方形的面积，所以剩余部分的表面积与原来大正方体的表面积相等。
- **步骤二：计算原来大正方体的表面积**
根据正方体的表面积公式$S = 6a^2$（其中$S$为正方体的表面积，$a$为正方体的棱长），已知大正方体的棱长$a = 8cm$，将其代入公式可得：
$S=6\times8^2 = 6\times64 = 384$（平方厘米）
【答案】：$384$

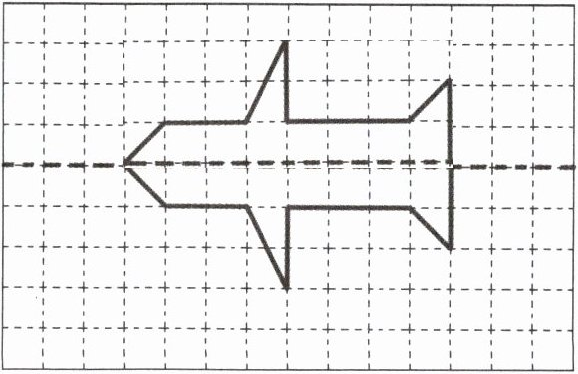
画出下面轴对称图形的另一半。

答案：