《2025年长江暑假作业崇文书局五年级数学北师大版》

3. 判断对错(对的画“√”,错的画“×”)。
(1)正方体的每一个面都有4条棱,正方体有6个面,所以正方体有24条棱。(×)
(2)如果长方体有两个相对的面是正方形,那么其余的四个面的面积都相等。(√)
(3)棱长是1分米的正方体纸盒放在桌子上,纸盒所占桌面的面积是1平方分米。(√)
(4)把一个长方体木料锯成两个长方体,一共增加了4个面。(×)

答案：
(1)×；
(2)√；
(3)√；
(4)×

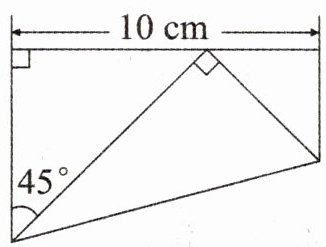
4. 如图,梯形的面积是多少平方厘米?

50平方厘米

答案： 【解析】：
已知图中有两个等腰直角三角形，所以梯形的上底与下底之和等于梯形的高，即$10$厘米。
根据梯形面积公式$S=(a + b)h÷2$（其中$a$为上底，$b$为下底，$h$为高），可得该梯形面积为$10×10÷2 = 50$（平方厘米）。
【答案】：$50$平方厘米

5. 请你做两个如下图所示的不同的硬纸盒(无盖)。做前先算一算,每个硬纸盒至少需要多少平方厘米的硬纸板?
第一个硬纸盒至少需要104平方厘米的硬纸板，第二个硬纸盒至少需要125平方厘米的硬纸板。

答案： 【解析】：
- 对于长方体硬纸盒（无盖）：
长方体表面积$S=(ab + ah+bh)×2$（$a$为长，$b$为宽，$h$为高），由于无盖，所以这个长方体硬纸盒的表面积$S = ab+(ah + bh)×2$。
已知$a = 8\mathrm{cm}$，$b = 4\mathrm{cm}$，$h = 3\mathrm{cm}$，代入可得：
$S=8×4+(8×3 + 4×3)×2$
$=32+(24 + 12)×2$
$=32 + 36×2$
$=32+72$
$=104\mathrm{cm}^{2}$。
对于正方体硬纸盒（无盖）：
正方体表面积$S = 6a^{2}$（$a$为棱长），由于无盖，所以这个正方体硬纸盒的表面积$S=5a^{2}$。
已知$a = 5\mathrm{cm}$，代入可得$S = 5×5×5=125\mathrm{cm}^{2}$。
【答案】：长方体硬纸盒至少需要$104$平方厘米的硬纸板，正方体硬纸盒至少需要$125$平方厘米的硬纸板。