2025年七彩假期暑假作业八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年七彩假期暑假作业八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列说法正确的是 (
A.对角线相等的平行四边形是菱形
B.有一组邻边相等的平行四边形是菱形
C.对角线相互垂直的四边形是菱形
D.有一个角是直角的平行四边形是菱形
B
)A.对角线相等的平行四边形是菱形
B.有一组邻边相等的平行四边形是菱形
C.对角线相互垂直的四边形是菱形
D.有一个角是直角的平行四边形是菱形
答案:
B
2. 如图,将$\triangle ABC沿BC方向平移得到\triangle DCE$,连结$AD$,下列条件能够判定四边形$ACED$为菱形的是 (
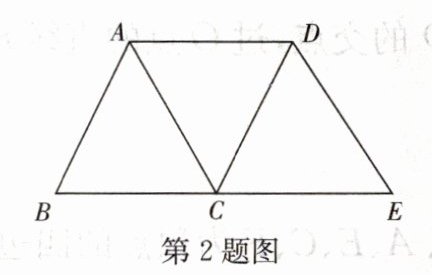
A.$AB= BC$
B.$AC= BC$
C.$\angle B= 60^{\circ}$
D.$\angle ACB= 60^{\circ}$
B
)
A.$AB= BC$
B.$AC= BC$
C.$\angle B= 60^{\circ}$
D.$\angle ACB= 60^{\circ}$
答案:
B
3. 如图,小红在作线段$AB$的垂直平分线时,是这样操作的:分别以点$A$、$B$为圆心,大于线段$AB$长度一半的长为半径画弧,相交于点$C$、$D$,则直线$CD$即为所求. 连结$AC$、$BC$、$AD$、$BD$,根据她的作图方法可知,四边形$ADBC$一定是 (

A.矩形
B.菱形
C.正方形
D.等腰梯形
B
)
A.矩形
B.菱形
C.正方形
D.等腰梯形
答案:
B
4. 如图,$CD与BE$互相垂直平分,$AD\perp DB$,$\angle BDE= 70^{\circ}$,则$\angle CAD= $

70^{\circ}
.
答案:
$70^{\circ}$
5. 顺次连结矩形四边中点所形成的四边形是
菱形
. 学校的一块菱形花园两对角线的长分别是$6m和8m$,则这个花园的面积为24cm^{2}
.
答案:
菱形 $24cm^{2}$
6. 如图,在$□ ABCD$中,$AC$为其对角线,过点$D作AC的平行线与BC的延长线交于点E$.
(1) 求证:$\triangle ABC\cong\triangle DCE$;
证明:因为四边形$ABCD$是平行四边形,所以$AB = DC$,$AB// DC$,则$\angle B=\angle DCE$。
又因为$AC// DE$,所以$\angle ACB=\angle E$。
在$\triangle ABC$和$\triangle DCE$中,$\begin{cases}\angle B=\angle DCE\\\angle ACB=\angle E\\AB = DC\end{cases}$,根据
(2) 若$AC= BC$,求证:四边形$ACED$为菱形.
证明:因为四边形$ABCD$是平行四边形,所以$AD// BC$,又因为$AC// DE$,所以四边形$ACED$是
因为$AC = BC$,$BC = AD$(平行四边形对边相等),所以$AC = AD$。
一组邻边相等的平行四边形是菱形,所以四边形$ACED$为菱形。
(1) 求证:$\triangle ABC\cong\triangle DCE$;
证明:因为四边形$ABCD$是平行四边形,所以$AB = DC$,$AB// DC$,则$\angle B=\angle DCE$。
又因为$AC// DE$,所以$\angle ACB=\angle E$。
在$\triangle ABC$和$\triangle DCE$中,$\begin{cases}\angle B=\angle DCE\\\angle ACB=\angle E\\AB = DC\end{cases}$,根据
AAS
(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ABC\cong\triangle DCE$。(2) 若$AC= BC$,求证:四边形$ACED$为菱形.
证明:因为四边形$ABCD$是平行四边形,所以$AD// BC$,又因为$AC// DE$,所以四边形$ACED$是
平行四边形
。因为$AC = BC$,$BC = AD$(平行四边形对边相等),所以$AC = AD$。
一组邻边相等的平行四边形是菱形,所以四边形$ACED$为菱形。
答案:
(1) 因为四边形$ABCD$是平行四边形,所以$AB = DC$,$AB// DC$,则$\angle B=\angle DCE$。
又因为$AC// DE$,所以$\angle ACB=\angle E$。
在$\triangle ABC$和$\triangle DCE$中,$\begin{cases}\angle B=\angle DCE\\\angle ACB=\angle E\\AB = DC\end{cases}$,根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ABC\cong\triangle DCE$。
(2) 因为四边形$ABCD$是平行四边形,所以$AD// BC$,又因为$AC// DE$,所以四边形$ACED$是平行四边形。
因为$AC = BC$,$BC = AD$(平行四边形对边相等),所以$AC = AD$。
一组邻边相等的平行四边形是菱形,所以四边形$ACED$为菱形。
(1) 因为四边形$ABCD$是平行四边形,所以$AB = DC$,$AB// DC$,则$\angle B=\angle DCE$。
又因为$AC// DE$,所以$\angle ACB=\angle E$。
在$\triangle ABC$和$\triangle DCE$中,$\begin{cases}\angle B=\angle DCE\\\angle ACB=\angle E\\AB = DC\end{cases}$,根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ABC\cong\triangle DCE$。
(2) 因为四边形$ABCD$是平行四边形,所以$AD// BC$,又因为$AC// DE$,所以四边形$ACED$是平行四边形。
因为$AC = BC$,$BC = AD$(平行四边形对边相等),所以$AC = AD$。
一组邻边相等的平行四边形是菱形,所以四边形$ACED$为菱形。
查看更多完整答案,请扫码查看


