《2025年七彩假期暑假作业八年级数学》

7. 如图,在$△ABC$中,$AB= AC$,将$△ABC绕点C顺时针旋转180^{\circ}得到△FEC$,连结$AE$、$BF$。当$∠ACB$为60度时,四边形$ABFE$为矩形。

答案： 60

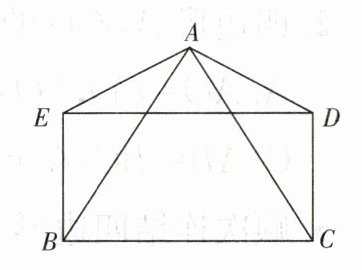
8. 如图,$AB= AC$,$AD= AE$,$DE= BC$,且$∠BAD= ∠CAE$。
求证：四边形$BCDE$是矩形。

证明：先证$\triangle ABE\cong\triangle ACD(SAS)$得$BE = CD$，结合$DE = BC$证四边形$BCDE$是平行四边形，再由$AB = AC$推出$\angle EBC=\angle DCB = 90^{\circ}$，从而证得四边形$BCDE$是矩形。

答案： 【解析】：
1. 首先证明$\triangle ABE\cong\triangle ACD$：
已知$\angle BAD = \angle CAE$，则$\angle BAD-\angle BAC=\angle CAE - \angle BAC$，即$\angle BAE=\angle CAD$。
在$\triangle ABE$和$\triangle ACD$中，$\left\{\begin{array}{l}AB = AC\\\angle BAE=\angle CAD\\AE = AD\end{array}\right.$，根据$SAS$（边角边）定理，可得$\triangle ABE\cong\triangle ACD$。
所以$\angle ABE=\angle ACD$，$BE = CD$。
2. 然后证明四边形$BCDE$是平行四边形：
因为$DE = BC$，$BE = CD$，根据“两组对边分别相等的四边形是平行四边形”，所以四边形$BCDE$是平行四边形。
3. 最后证明平行四边形$BCDE$是矩形：
因为$AB = AC$，所以$\angle ABC=\angle ACB$。
又因为$\angle ABE=\angle ACD$，所以$\angle ABC+\angle ABE=\angle ACB+\angle ACD$，即$\angle EBC=\angle DCB$。
由于四边形$BCDE$是平行四边形，所以$EB// DC$，则$\angle EBC+\angle DCB = 180^{\circ}$。
所以$\angle EBC=\angle DCB = 90^{\circ}$。
根据“有一个角是直角的平行四边形是矩形”，所以四边形$BCDE$是矩形。
【答案】：
先证$\triangle ABE\cong\triangle ACD(SAS)$得$BE = CD$，结合$DE = BC$证四边形$BCDE$是平行四边形，再由$AB = AC$推出$\angle EBC=\angle DCB = 90^{\circ}$，从而证得四边形$BCDE$是矩形。

9. 如图,将平行四边形$ABCD的边DC延长至点E$,使$CE= DC$,连结$AE$,交$BC于点F$。
(1)求证：$△ABF≌△ECF$；
(2)连结$AC$、$BE$,则当$∠AFC与∠D$满足什么条件时,四边形$ABEC$是矩形？请说明理由。
(1) 证明：在平行四边形 $ ABCD $ 中，$ AB // CD $，$ AB = CD $，
$ \therefore \angle BAE = \angle AEC $。
又 $ \because CE = CD $，$ \therefore AB = CE $，
在 $ \triangle ABF $ 和 $ \triangle ECF $ 中，
$ \left\{ \begin{array} { l } { \angle AFB = \angle EFC, } \\ { \angle BAF = \angle CEF, } \\ { AB = CE, } \end{array} \right. $
$ \therefore \triangle ABF \cong \triangle ECF $(AAS)；
(2) 解：当$∠AFC= $$2∠D$时，四边形$ABEC$是矩形。
$ \because $ 四边形 $ ABCD $ 是平行四边形，
$ \therefore BC // AD $，$ \angle BCE = \angle D $。
由题意易得 $ AB // EC $，$ AB = EC $，
$ \therefore $ 四边形 $ ABEC $ 是平行四边形。
$ \because \angle AFC = \angle FEC + \angle BCE $，
$ \therefore $ 当 $ \angle AFC = 2 \angle D $ 时，则有 $ \angle FEC = \angle FCE $，
$ \therefore FC = FE $，$ \therefore $ 四边形 $ ABEC $ 是矩形(对角线相等的平行四边形是矩形)。

答案：
(1) 证明：在平行四边形 $ ABCD $ 中，$ AB // CD $，$ AB = CD $，
$ \therefore \angle BAE = \angle AEC $。
又 $ \because CE = CD $，$ \therefore AB = CE $，
在 $ \triangle ABF $ 和 $ \triangle ECF $ 中，
$ \left\{ \begin{array} { l } { \angle AFB = \angle EFC, } \\ { \angle BAF = \angle CEF, } \\ { AB = CE, } \end{array} \right. $
$ \therefore \triangle ABF \cong \triangle ECF $；
(2) 解：当 $ \angle AFC = 2 \angle D $ 时，四边形 $ ABEC $ 是矩形。
$ \because $ 四边形 $ ABCD $ 是平行四边形，
$ \therefore BC // AD $，$ \angle BCE = \angle D $。
由题意易得 $ AB // EC $，$ AB = EC $，
$ \therefore $ 四边形 $ ABEC $ 是平行四边形。
$ \because \angle AFC = \angle FEC + \angle BCE $，
$ \therefore $ 当 $ \angle AFC = 2 \angle D $ 时，则有 $ \angle FEC = \angle FCE $，
$ \therefore FC = FE $，$ \therefore $ 四边形 $ ABEC $ 是矩形。