《2025年七彩假期暑假作业八年级数学》

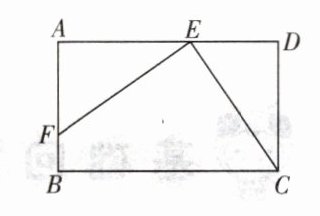
6. 如图,已知矩形 ABCD 中,E 是 AD 上的一点,F 是 AB 上的一点,$EF⊥EC$,且$EF= EC,DE= 4cm$,矩形 ABCD 的周长为 32 cm,求 AE 的长.

6 cm

答案： $ AE = 6 \text{ cm} $.

7. (铅山县二模)如图,在矩形 ABCD 中,EF 经过对角线 BD 的中点 O,分别交 AD、BC 于点 E、F.
(1)求证:$△BOF\cong △DOE;$
证明：因为四边形$ABCD$是矩形，所以$AD// BC$，则$\angle EDO=\angle FBO$。又因为$O$是$BD$的中点，所以$OB = OD$。在$\triangle BOF$和$\triangle DOE$中，$\left\{\begin{array}{l}\angle EDO=\angle FBO\\ OD = OB\\ \angle DOE=\angle BOF\end{array}\right.$（对顶角相等）。根据ASA判定定理，可得$\triangle BOF\cong\triangle DOE$。
(2)若$AB= 4cm,AD= 5cm$,当$EF⊥BD$时,求四边形 ABFE 的面积.
解：因为$\triangle BOF\cong\triangle DOE$，所以$S_{\triangle BOF}=S_{\triangle DOE}$。那么$S_{四边形ABFE}=S_{四边形ABFO}+S_{\triangle BOF}=S_{四边形ABFO}+S_{\triangle DOE}=S_{梯形ABOD}$。已知$AB = 4cm$，$AD = 5cm$，$S_{矩形ABCD}=AB× AD=4×5 = 20cm^{2}$，$S_{\triangle ABD}=\frac{1}{2}S_{矩形ABCD}$（矩形的对角线把矩形分成两个面积相等的三角形），$S_{四边形ABFE}=S_{\triangle ABD}$，所以$S_{四边形ABFE}=\frac{1}{2}×4×5 =$10$cm^{2}$。

答案： 1. （1）证明：
因为四边形$ABCD$是矩形，所以$AD// BC$，则$\angle EDO=\angle FBO$。
又因为$O$是$BD$的中点，所以$OB = OD$。
在$\triangle BOF$和$\triangle DOE$中，$\left\{\begin{array}{l}\angle EDO=\angle FBO\\ OD = OB\\ \angle DOE=\angle BOF\end{array}\right.$（对顶角相等）。
根据$ASA$（角 - 边 - 角）判定定理，可得$\triangle BOF\cong\triangle DOE$。
2. （2）解：
因为$\triangle BOF\cong\triangle DOE$，所以$S_{\triangle BOF}=S_{\triangle DOE}$。
那么$S_{四边形ABFE}=S_{四边形ABFO}+S_{\triangle BOF}=S_{四边形ABFO}+S_{\triangle DOE}=S_{梯形ABOD}$。
已知$AB = 4cm$，$AD = 5cm$，$O$是$BD$中点，根据梯形面积公式$S=\frac{(a + b)h}{2}$（这里$a = AB$，$b = OD$，$h = AB$，$OD=\frac{1}{2}BD$，在矩形$ABCD$中，$BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{4^{2}+5^{2}}=\sqrt{16 + 25}=\sqrt{41}$，$OD=\frac{\sqrt{41}}{2}$，但我们换一种思路）。
因为$S_{矩形ABCD}=AB× AD=4×5 = 20cm^{2}$，$S_{\triangle ABD}=\frac{1}{2}S_{矩形ABCD}$（矩形的对角线把矩形分成两个面积相等的三角形），$S_{四边形ABFE}=S_{\triangle ABD}$（因为$S_{四边形ABFE}=S_{梯形ABOD}$，$S_{梯形ABOD}=S_{\triangle ABD}$）。
所以$S_{四边形ABFE}=\frac{1}{2}×4×5 = 10cm^{2}$。
综上，（1）已证$\triangle BOF\cong\triangle DOE$；（2）四边形$ABFE$的面积是$10cm^{2}$。