1. 一个长方体棱长的和是84 cm,它的长是8 cm,宽是6 cm,它的高是多少厘米?
答案:
$84÷4 - 8 - 6 = 7(cm)$
2. 要用硬纸板做一个长方体盒子,盒子底面是边长为4 dm 的正方形,盒子高0.5 m,至少需要多少平方分米的硬纸板?(盒子无盖)
答案:
$0.5m = 5dm$ $4×5×4 + 4×4 = 96(dm^{2})$
同学们,如何判断一个图形折叠后能否围成正方体?
1. 可以利用空间想象或用实物图折一折。
2. 可以依据展开图的特征判断。
3. 看展开图是否形如$(1,4,1),(2,3,1),(2,2,2),(3,3)$所示。
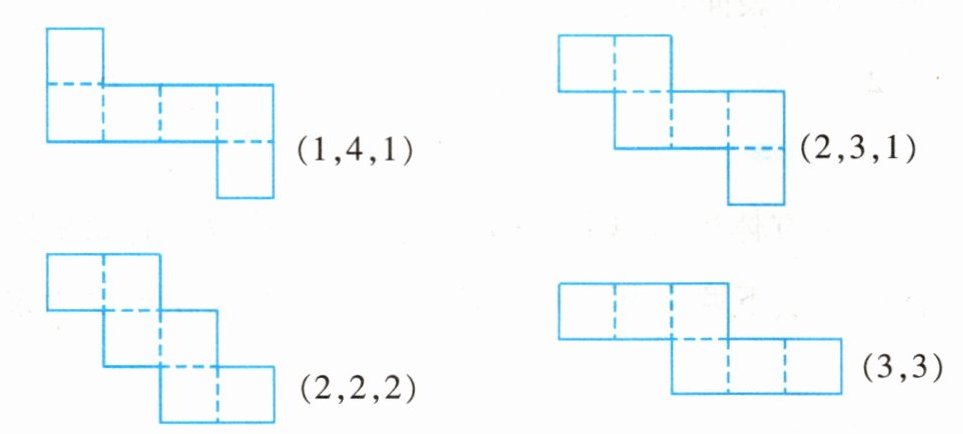
聪明的小朋友,试试看,你还有其他小妙招吗?
1. 可以利用空间想象或用实物图折一折。
2. 可以依据展开图的特征判断。
3. 看展开图是否形如$(1,4,1),(2,3,1),(2,2,2),(3,3)$所示。

聪明的小朋友,试试看,你还有其他小妙招吗?
1. 看展开图中是否有“田”字形和“凹”字形,若有则不能围成正方体。2. 检查展开图中相对面的分布是否符合间隔出现的规律,不符合则不能围成正方体。
答案:
【解析】:判断一个图形折叠后能否围成正方体,首先可以通过空间想象在脑海中模拟折叠过程,或者动手用实物图折一折,直观地看是否能围成正方体;依据展开图的特征判断也是常用方法,常见的能围成正方体的展开图有$(1,4,1)$、$(2,3,1)$、$(2,2,2)$、$(3,3)$这些类型。除此之外,还可以看展开图中是否存在“田”字形和“凹”字形,若存在则不能围成正方体,因为“田”字形和“凹”字形在折叠时会出现面的重叠或无法封闭的情况;也可以检查相对面的情况,正方体展开图中相对面是间隔出现的,如果展开图中相对面的分布不符合这一规律,那么就不能围成正方体。
【答案】:1. 看展开图中是否有“田”字形和“凹”字形,若有则不能围成正方体。2. 检查展开图中相对面的分布是否符合间隔出现的规律,不符合则不能围成正方体。
【答案】:1. 看展开图中是否有“田”字形和“凹”字形,若有则不能围成正方体。2. 检查展开图中相对面的分布是否符合间隔出现的规律,不符合则不能围成正方体。
算一算
$\frac{3}{10} + \frac{7}{10}=$
$\frac{5}{6} - \frac{1}{2}=$
$\frac{5}{6} + \frac{1}{10}=$
$\frac{4}{7} - \frac{1}{3}=$
$\frac{2}{3} + \frac{7}{9}=$
$\frac{7}{8} - \frac{3}{4}=$
$\frac{3}{5} + \frac{3}{8}=$
$4 - \frac{1}{2}=$
$\frac{1}{2} + \frac{2}{3}=$
$\frac{2}{3} - \frac{1}{4}=$
$\frac{3}{10} + \frac{7}{10}=$
1
$\frac{5}{6} - \frac{1}{2}=$
$\frac{1}{3}$
$\frac{5}{6} + \frac{1}{10}=$
$\frac{14}{15}$
$\frac{4}{7} - \frac{1}{3}=$
$\frac{5}{21}$
$\frac{2}{3} + \frac{7}{9}=$
$\frac{13}{9}$
$\frac{7}{8} - \frac{3}{4}=$
$\frac{1}{8}$
$\frac{3}{5} + \frac{3}{8}=$
$\frac{39}{40}$
$4 - \frac{1}{2}=$
$\frac{7}{2}$
$\frac{1}{2} + \frac{2}{3}=$
$\frac{7}{6}$
$\frac{2}{3} - \frac{1}{4}=$
$\frac{5}{12}$
答案:
【解析】:
1. 同分母分数相加,分母不变,分子相加,$\frac{3}{10}+\frac{7}{10}=\frac{3 + 7}{10}=\frac{10}{10}=1$。
2. 先通分,$\frac{1}{2}=\frac{3}{6}$,再相减,$\frac{5}{6}-\frac{1}{2}=\frac{5}{6}-\frac{3}{6}=\frac{5 - 3}{6}=\frac{2}{6}=\frac{1}{3}$。
3. 先通分,$\frac{5}{6}=\frac{25}{30}$,$\frac{1}{10}=\frac{3}{30}$,再相加,$\frac{5}{6}+\frac{1}{10}=\frac{25}{30}+\frac{3}{30}=\frac{25 + 3}{30}=\frac{28}{30}=\frac{14}{15}$。
4. 先通分,$\frac{4}{7}=\frac{12}{21}$,$\frac{1}{3}=\frac{7}{21}$,再相减,$\frac{4}{7}-\frac{1}{3}=\frac{12}{21}-\frac{7}{21}=\frac{12 - 7}{21}=\frac{5}{21}$。
5. 先通分,$\frac{2}{3}=\frac{6}{9}$,再相加,$\frac{2}{3}+\frac{7}{9}=\frac{6}{9}+\frac{7}{9}=\frac{6 + 7}{9}=\frac{13}{9}$。
6. 先通分,$\frac{3}{4}=\frac{6}{8}$,再相减,$\frac{7}{8}-\frac{3}{4}=\frac{7}{8}-\frac{6}{8}=\frac{7 - 6}{8}=\frac{1}{8}$。
7. 先通分,$\frac{3}{5}=\frac{24}{40}$,$\frac{3}{8}=\frac{15}{40}$,再相加,$\frac{3}{5}+\frac{3}{8}=\frac{24}{40}+\frac{15}{40}=\frac{24+15}{40}=\frac{39}{40}$。
8. 把$4$化为$\frac{8}{2}$,再相减,$4-\frac{1}{2}=\frac{8}{2}-\frac{1}{2}=\frac{8 - 1}{2}=\frac{7}{2}$。
9. 先通分,$\frac{1}{2}=\frac{3}{6}$,$\frac{2}{3}=\frac{4}{6}$,再相加,$\frac{1}{2}+\frac{2}{3}=\frac{3}{6}+\frac{4}{6}=\frac{3 + 4}{6}=\frac{7}{6}$。
10. 先通分,$\frac{2}{3}=\frac{8}{12}$,$\frac{1}{4}=\frac{3}{12}$,再相减,$\frac{2}{3}-\frac{1}{4}=\frac{8}{12}-\frac{3}{12}=\frac{8 - 3}{12}=\frac{5}{12}$。
【答案】:1. $1$ 2. $\frac{1}{3}$ 3. $\frac{14}{15}$ 4. $\frac{5}{21}$ 5. $\frac{13}{9}$ 6. $\frac{1}{8}$ 7. $\frac{39}{40}$ 8. $\frac{7}{2}$ 9. $\frac{7}{6}$ 10. $\frac{5}{12}$
1. 同分母分数相加,分母不变,分子相加,$\frac{3}{10}+\frac{7}{10}=\frac{3 + 7}{10}=\frac{10}{10}=1$。
2. 先通分,$\frac{1}{2}=\frac{3}{6}$,再相减,$\frac{5}{6}-\frac{1}{2}=\frac{5}{6}-\frac{3}{6}=\frac{5 - 3}{6}=\frac{2}{6}=\frac{1}{3}$。
3. 先通分,$\frac{5}{6}=\frac{25}{30}$,$\frac{1}{10}=\frac{3}{30}$,再相加,$\frac{5}{6}+\frac{1}{10}=\frac{25}{30}+\frac{3}{30}=\frac{25 + 3}{30}=\frac{28}{30}=\frac{14}{15}$。
4. 先通分,$\frac{4}{7}=\frac{12}{21}$,$\frac{1}{3}=\frac{7}{21}$,再相减,$\frac{4}{7}-\frac{1}{3}=\frac{12}{21}-\frac{7}{21}=\frac{12 - 7}{21}=\frac{5}{21}$。
5. 先通分,$\frac{2}{3}=\frac{6}{9}$,再相加,$\frac{2}{3}+\frac{7}{9}=\frac{6}{9}+\frac{7}{9}=\frac{6 + 7}{9}=\frac{13}{9}$。
6. 先通分,$\frac{3}{4}=\frac{6}{8}$,再相减,$\frac{7}{8}-\frac{3}{4}=\frac{7}{8}-\frac{6}{8}=\frac{7 - 6}{8}=\frac{1}{8}$。
7. 先通分,$\frac{3}{5}=\frac{24}{40}$,$\frac{3}{8}=\frac{15}{40}$,再相加,$\frac{3}{5}+\frac{3}{8}=\frac{24}{40}+\frac{15}{40}=\frac{24+15}{40}=\frac{39}{40}$。
8. 把$4$化为$\frac{8}{2}$,再相减,$4-\frac{1}{2}=\frac{8}{2}-\frac{1}{2}=\frac{8 - 1}{2}=\frac{7}{2}$。
9. 先通分,$\frac{1}{2}=\frac{3}{6}$,$\frac{2}{3}=\frac{4}{6}$,再相加,$\frac{1}{2}+\frac{2}{3}=\frac{3}{6}+\frac{4}{6}=\frac{3 + 4}{6}=\frac{7}{6}$。
10. 先通分,$\frac{2}{3}=\frac{8}{12}$,$\frac{1}{4}=\frac{3}{12}$,再相减,$\frac{2}{3}-\frac{1}{4}=\frac{8}{12}-\frac{3}{12}=\frac{8 - 3}{12}=\frac{5}{12}$。
【答案】:1. $1$ 2. $\frac{1}{3}$ 3. $\frac{14}{15}$ 4. $\frac{5}{21}$ 5. $\frac{13}{9}$ 6. $\frac{1}{8}$ 7. $\frac{39}{40}$ 8. $\frac{7}{2}$ 9. $\frac{7}{6}$ 10. $\frac{5}{12}$
查看更多完整答案,请扫码查看


