《2025年名师学案九年级物理下册人教版》

9.有两个灯泡，$L_{1}$标有“6V　3W”字样，$L_{2}$没有标记，但测得它的电阻是6 $\Omega$，把它们串联后接入某一电路时，灯$L_{1}$、$L_{2}$均能正常发光，那么这个电路两端的电压为______V，$L_{2}$的额定功率是______W。

答案： 9 1.5

10.在如图所示的电路中，灯泡L标有“3V　0.9W”的字样，$R = 20$ $\Omega$。当灯泡正常发光时，电路消耗的总功率是______W。

答案： 2.7

11.如图,电阻$R_{1} = 20$ $\Omega$，$R_{2} =$ 10 $\Omega$，当开关S闭合时电流表示数为0.3A,则$R_{2}$消耗
　　的电功率为______W。

答案： 3.6

12.(中考·南充)将一段电阻丝接入电路中，测得其两端电压为12V，通过的电流为3A，则该电阻丝电阻为______$\Omega$；若将该电阻丝两端电压由12V降至6V，则电功率变化了______W。

答案： 4 27

13.(变式拓展1)一灯泡标有“6V　3W”的字样，现仅有8V的电源，要使小灯泡正常发光，应该给小灯泡串联一个______$\Omega$的电阻，此时电路的总功率为______W。

答案： 4 4

14.(变式拓展2)把标有“6V　3W”和“6V 6W”的两个灯泡串联接入电路中，在保证安全使用的情况下让其中一个灯泡正常发光，忽略温度对灯丝电阻的影响，则电源两端电压是______V，此时两灯消耗的总功率为______W。

答案： 9 4.5

15.(2024·达州)如图所示，电源电压恒定不变。
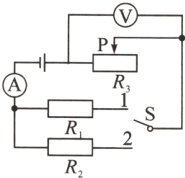
电流表量程0～3A,电压表量程0～15V,滑动变阻器$R_{3}$标有“40 $\Omega$ 1A”字样，已知$R_{1}$阻值为30 $\Omega$。当滑片P置于最左端，开关S置于1时，电流表示数为0.8A；当滑片P置于中点，开关S先后置于1、2时，电流表示数之比为4∶5。求:
　(1)电源电压；
　(2)电阻$R_{2}$的阻值；
　(3)当S置于2时，在保证电路安全的前提下，整个电路的最小电功率。
　　　　　　　　　　　

答案： 解：
(1)当滑片 P 置于最左端，开关 S 置于 1 时，滑动变阻器接入电路的阻值为 0，电路为只有$R_{1}$的简单电路，此时电流表示数为 0.8A，则电源电压为：$U = I_{0}R_{1}=0.8A×30Ω = 24V$；
(2)当滑片 P 置于中点，开关 S 先后置于 1、2 时，电阻$R_{1}$和$R_{2}$分别与滑动变阻器串联，此时电路中的电流分别为：$I_{1}=\frac{U}{R_{1}+\frac{1}{2}R_{3}}=\frac{24V}{30Ω+\frac{1}{2}×40Ω}=0.48A$，$I_{2}=\frac{U}{R_{2}+\frac{1}{2}R_{3}}=\frac{24V}{R_{2}+\frac{1}{2}×40Ω}$，因电流表示数之比为 4 : 5，即$I_{2}=\frac{5}{4}I_{1}=\frac{5}{4}×0.48A=\frac{24V}{R_{2}+\frac{1}{2}×40Ω}$，解得：$R_{2}=20Ω$；
(3)当 S 置于 2 时，滑动变阻器和$R_{2}$串联，电压表测滑动变阻器两端电压，电流表测电路中的电流；当电压表示数最大时，滑动变阻器接入电路的阻值最大，此时电路的电流最小，整个电路的功率最小；由题意可知，电压表最大示数为 15V，根据串联电路电压规律可知，此时$R_{2}$两端电压为$U_{2}=U - U_{V}=24V - 15V = 9V$，通过$R_{2}$的电流为：$I_{2}'=\frac{U_{2}}{R_{2}}=\frac{9V}{20Ω}=0.45A$，根据串联电路电流特点和$P = UI$可知，整个电路的最小电功率为：$P = UI_{2}'=24V×0.45A = 10.8W$。