《2025年教材全练四年级数学下册人教版天津专版》

1. 把下列图形的序号填在相应的位置。

直角三角形：________
锐角三角形：________
钝角三角形：________

答案： 直角三角形:①④ 锐角三角形:③⑤
钝角三角形:②⑥

2. 填一填。
(1)(宁波市北仑区)一个等腰三角形的一个底角是40°，这个三角形按角分是( )三角形。
(2)一个三角形中，最多有( )个钝角，最多有( )个锐角。

答案：
(1)钝角
【解析】根据题意可求出这个三角形的顶角是180° - 40°×2 = 100°，即这个三角形有一个角是钝角，所以这个三角形是钝角三角形。
(2)1 3

3. 选一选。
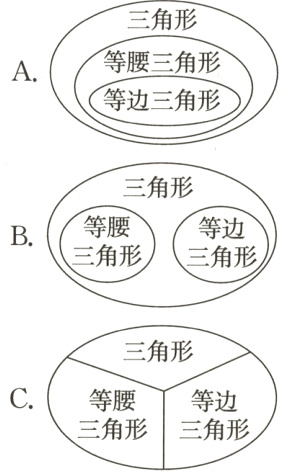
(1)(舟山市普陀区)将三角形按边的特点进行分类，正确的是( )。
　

答案：
(1)A
【解析】有两条边相等的三角形叫作等腰三角形，等边三角形是等腰三角形的特殊情况。

(2)如果一个等腰三角形的一条边长5cm，另一条边长10cm，那么这个等腰三角形的周长是( )cm。
A. 15 B. 20 C. 25

答案：
(2)C
【解析】由“三角形任意两边的和大于第三边”可知，这个等腰三角形的腰长是10 cm，所以周长是10 + 10 + 5 = 25(cm)。

4. 下面的三角形都被一张纸遮住了下半部分，你能确定它们各是什么三角形吗?

答案： a三角形是钝角三角形；b三角形是直角三角形；不能确定c三角形是什么三角形。
【解析】a三角形露出的角是钝角，所以它一定是钝角三角形；b三角形露出的角是直角，所以它一定是直角三角形；c三角形只露出1个锐角，所以不能确定它是什么三角形。

5. 按要求将五边形分成3个三角形，画一画。
(1)使其中两个三角形是直角三角形。

(2)使其中两个三角形是钝角三角形。

答案：
(画法不唯一)
(1)

【解析】观察图形可知，先连接CE，四边形ABCE是一个正方形，再连接BE或AC即可。
(2)

【解析】可以保留五边形中的两个钝角∠C和∠E，连接BD和AD即可。