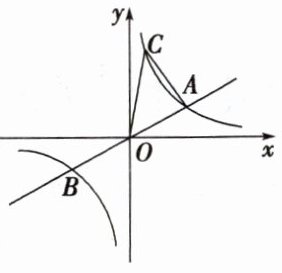
9. 如图,已知直线$y = \frac{2}{3}x$与双曲线$y = \frac{k}{x}(k > 0)$的图象交于$A$,$B$两点,$A$点的横坐标为3,则下列结论:①$k = 6$;②$A$点与$B$点关于原点$O$中心对称;③关于$x$的不等式$\frac{2}{3}x - \frac{k}{x} < 0$的解集为$x < -3$,或$0 < x < 3$;④若双曲线$y = \frac{k}{x}(k > 0)$上有一点$C$,其纵坐标为6,则$\triangle AOC$的面积为8. 其中正确结论的个数有( )
A. 4个
B. 3个
C. 2个
D. 1个

A. 4个
B. 3个
C. 2个
D. 1个
答案:
A
∵直线 $y=\frac{2}{3}x$ 与双曲线 $y=\frac{k}{x}(k>0)$ 的图象交于 $A$,$B$ 两点,$A$ 点的横坐标为 $3$,
∴点 $A$ 的纵坐标为 $y=\frac{2}{3}\times3 = 2$,
∴点 $A(3,2)$,
∴ $k = 3\times2 = 6$,故①正确;
∵直线 $y=\frac{2}{3}x$ 与双曲线 $y=\frac{k}{x}(k>0)$ 的图象都是中心对称图形,
∴ $A$ 点与 $B$ 点关于原点 $O$ 中心对称,故②正确;
∴点 $B(-3,-2)$, 由图可知,关于 $x$ 的不等式 $\frac{2}{3}x-\frac{k}{x}<0$ 的解集为 $x<-3$,或 $0<x<3$,故③正确; 如图,过点 $C$ 作 $CD\perp x$ 轴于点 $D$,过点 $A$ 作 $AE\perp x$ 轴于点 $E$,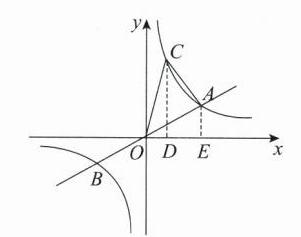
∵点 $C$ 的纵坐标为 $6$,
∴把 $y = 6$ 代入 $y=\frac{6}{x}$,得 $x = 1$,
∴点 $C(1,6)$,
∴ $S_{\triangle AOC}=S_{\triangle OCD}+S_{梯形AEDC}-S_{\triangle AOE}=S_{梯形AEDC}=\frac{1}{2}\times(2 + 6)\times(3 - 1)=8$,故④正确。
A
∵直线 $y=\frac{2}{3}x$ 与双曲线 $y=\frac{k}{x}(k>0)$ 的图象交于 $A$,$B$ 两点,$A$ 点的横坐标为 $3$,
∴点 $A$ 的纵坐标为 $y=\frac{2}{3}\times3 = 2$,
∴点 $A(3,2)$,
∴ $k = 3\times2 = 6$,故①正确;
∵直线 $y=\frac{2}{3}x$ 与双曲线 $y=\frac{k}{x}(k>0)$ 的图象都是中心对称图形,
∴ $A$ 点与 $B$ 点关于原点 $O$ 中心对称,故②正确;
∴点 $B(-3,-2)$, 由图可知,关于 $x$ 的不等式 $\frac{2}{3}x-\frac{k}{x}<0$ 的解集为 $x<-3$,或 $0<x<3$,故③正确; 如图,过点 $C$ 作 $CD\perp x$ 轴于点 $D$,过点 $A$ 作 $AE\perp x$ 轴于点 $E$,

∵点 $C$ 的纵坐标为 $6$,
∴把 $y = 6$ 代入 $y=\frac{6}{x}$,得 $x = 1$,
∴点 $C(1,6)$,
∴ $S_{\triangle AOC}=S_{\triangle OCD}+S_{梯形AEDC}-S_{\triangle AOE}=S_{梯形AEDC}=\frac{1}{2}\times(2 + 6)\times(3 - 1)=8$,故④正确。
10. 反比例函数$y = \frac{k}{x}(k \neq 0)$的图象上有一点$P(2,n)$,将点$P$向右平移1个单位长度,再向下平移1个单位长度得到点$Q$. 若点$Q$也在该函数的图象上,则$n =$_______.
答案:
3
∵点 $P$ 的坐标为 $(2,n)$,将点 $P$ 向右平移 $1$ 个单位长度,再向下平移 $1$ 个单位长度得到点 $Q$,
∴点 $Q$ 的坐标为 $(3,n - 1)$, 依题意得 $k = 2n = 3(n - 1)$,解得 $n = 3$。
∵点 $P$ 的坐标为 $(2,n)$,将点 $P$ 向右平移 $1$ 个单位长度,再向下平移 $1$ 个单位长度得到点 $Q$,
∴点 $Q$ 的坐标为 $(3,n - 1)$, 依题意得 $k = 2n = 3(n - 1)$,解得 $n = 3$。
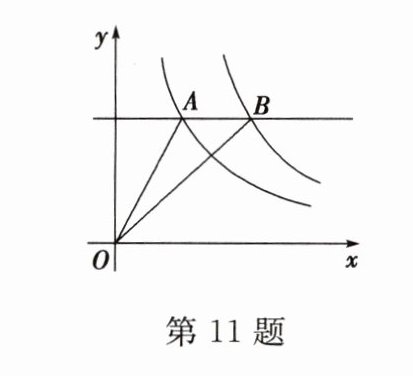
11. 反比例函数$y = \frac{k_1}{x}$和$y = \frac{k_2}{x}(k_1 < k_2)$在第一象限的图象如图所示,直线$AB // x$轴,并分别交两条曲线于$A$,$B$两点,若$S_{\triangle AOB} = 2$,则$k_2 - k_1$的值为_______.

答案:
4 设点 $A$ 的纵坐标为 $n$,
∵ $AB// x$ 轴,
∴点 $B$ 的纵坐标为 $n$,
∵点 $A$,点 $B$ 分别在 $y=\frac{k_{1}}{x}$,$y=\frac{k_{2}}{x}(k_{1}<k_{2})$ 的第一象限的图象上,
∴点 $A$,点 $B$ 的横坐标分别为 $\frac{k_{1}}{n}$,$\frac{k_{2}}{n}$,
∵ $S_{\triangle AOB}=2$,
∴ $\frac{1}{2}(\frac{k_{2}}{n}-\frac{k_{1}}{n})n = 2$。
∴ $k_{2}-k_{1}=4$。
∵ $AB// x$ 轴,
∴点 $B$ 的纵坐标为 $n$,
∵点 $A$,点 $B$ 分别在 $y=\frac{k_{1}}{x}$,$y=\frac{k_{2}}{x}(k_{1}<k_{2})$ 的第一象限的图象上,
∴点 $A$,点 $B$ 的横坐标分别为 $\frac{k_{1}}{n}$,$\frac{k_{2}}{n}$,
∵ $S_{\triangle AOB}=2$,
∴ $\frac{1}{2}(\frac{k_{2}}{n}-\frac{k_{1}}{n})n = 2$。
∴ $k_{2}-k_{1}=4$。
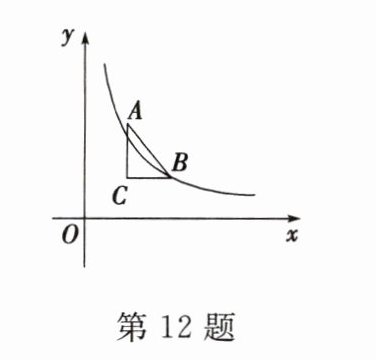
12. 如图,$\triangle ABC$在第一象限内,$\angle C = 90^{\circ}$,$BC // x$轴,点$C(2,2)$,$AB$所在直线的函数解析式是$y = - \frac{2}{3}x + 6$. 当反比例函数$y = \frac{k}{x}$的图象与$\triangle ABC$有交点时,$k$的取值范围是_______.

答案:
$4\leqslant k\leqslant\frac{27}{2}$
∵ $\triangle ABC$ 在第一象限内,$\angle C = 90^{\circ}$,$BC// x$ 轴,点 $C(2,2)$,
∴把 $x = 2$ 代入 $y=-\frac{2}{3}x + 6$,得 $y=-\frac{2}{3}\times2 + 6=\frac{14}{3}$, 把 $y = 2$ 代入 $y=-\frac{2}{3}x + 6$,得 $-\frac{2}{3}x + 6 = 2$, 解得 $x = 6$,
∴ $A(2,\frac{14}{3})$,$B(6,2)$, 根据反比例函数系数的几何意义,当反比例函数的图象与点 $C$ 相交时,$k$ 值最小,此时 $k = 2\times2 = 4$。 当反比例函数的图象与线段 $AB$ 有交点时, 则 $\frac{k}{x}=-\frac{2}{3}x + 6$, 即 $k=x(-\frac{2}{3}x + 6)=-\frac{2}{3}x^{2}+6x=-\frac{2}{3}(x-\frac{9}{2})^{2}+\frac{27}{2}$,
∵ $2\leqslant x\leqslant6$,
∴当 $x=\frac{9}{2}$ 时,$k$ 值最大, 此时交点坐标为 $(\frac{9}{2},3)$,则 $k=\frac{9}{2}\times3=\frac{27}{2}$, 因此,$k$ 的取值范围是 $4\leqslant k\leqslant\frac{27}{2}$。
∵ $\triangle ABC$ 在第一象限内,$\angle C = 90^{\circ}$,$BC// x$ 轴,点 $C(2,2)$,
∴把 $x = 2$ 代入 $y=-\frac{2}{3}x + 6$,得 $y=-\frac{2}{3}\times2 + 6=\frac{14}{3}$, 把 $y = 2$ 代入 $y=-\frac{2}{3}x + 6$,得 $-\frac{2}{3}x + 6 = 2$, 解得 $x = 6$,
∴ $A(2,\frac{14}{3})$,$B(6,2)$, 根据反比例函数系数的几何意义,当反比例函数的图象与点 $C$ 相交时,$k$ 值最小,此时 $k = 2\times2 = 4$。 当反比例函数的图象与线段 $AB$ 有交点时, 则 $\frac{k}{x}=-\frac{2}{3}x + 6$, 即 $k=x(-\frac{2}{3}x + 6)=-\frac{2}{3}x^{2}+6x=-\frac{2}{3}(x-\frac{9}{2})^{2}+\frac{27}{2}$,
∵ $2\leqslant x\leqslant6$,
∴当 $x=\frac{9}{2}$ 时,$k$ 值最大, 此时交点坐标为 $(\frac{9}{2},3)$,则 $k=\frac{9}{2}\times3=\frac{27}{2}$, 因此,$k$ 的取值范围是 $4\leqslant k\leqslant\frac{27}{2}$。
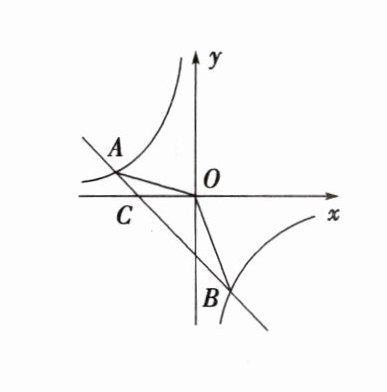
13. 已知一次函数$y = kx + b$和反比例函数$y = \frac{m}{x}$的图象相交于$A(-4,2)$,$B(n,-4)$两点.
(1)求一次函数和反比例函数的解析式;
(2)求$\triangle AOB$的面积;
(3)观察图象,直接写出不等式$kx + b - \frac{m}{x} < 0$的解集.
(1)求一次函数和反比例函数的解析式;
(2)求$\triangle AOB$的面积;
(3)观察图象,直接写出不等式$kx + b - \frac{m}{x} < 0$的解集.

答案:
解:
(1)
∵点 $A(-4,2)$ 在反比例函数 $y=\frac{m}{x}$ 的图象上,
∴ $2=\frac{m}{-4}$,解得 $m=-8$,
∴反比例函数的解析式为 $y=-\frac{8}{x}$。
∵点 $B(n,-4)$ 在反比例函数 $y=-\frac{8}{x}$ 的图象上,
∴ $-4=-\frac{8}{n}$,解得 $n = 2$。
∴ $B(2,-4)$,
∵点 $A(-4,2)$ 和点 $B(2,-4)$ 在一次函数 $y = kx + b$ 的图象上,
∴ $\begin{cases}-4k + b = 2\\2k + b=-4\end{cases}$,解得 $\begin{cases}k=-1\\b=-2\end{cases}$,
∴一次函数的解析式为 $y=-x - 2$;
(2)将 $y = 0$ 代入 $y=-x - 2$,得 $x=-2$, 即直线 $y=-x - 2$ 与 $x$ 轴交于点 $C(-2,0)$,
∴ $S_{\triangle AOB}=S_{\triangle AOC}+S_{\triangle BOC}=\frac{1}{2}\times2\times2+\frac{1}{2}\times2\times4 = 6$, 即 $\triangle AOB$ 的面积是 $6$;
(3)由图可得,不等式 $kx + b-\frac{m}{x}<0$ 的解集为 $x>2$,或 $-4<x<0$。
(1)
∵点 $A(-4,2)$ 在反比例函数 $y=\frac{m}{x}$ 的图象上,
∴ $2=\frac{m}{-4}$,解得 $m=-8$,
∴反比例函数的解析式为 $y=-\frac{8}{x}$。
∵点 $B(n,-4)$ 在反比例函数 $y=-\frac{8}{x}$ 的图象上,
∴ $-4=-\frac{8}{n}$,解得 $n = 2$。
∴ $B(2,-4)$,
∵点 $A(-4,2)$ 和点 $B(2,-4)$ 在一次函数 $y = kx + b$ 的图象上,
∴ $\begin{cases}-4k + b = 2\\2k + b=-4\end{cases}$,解得 $\begin{cases}k=-1\\b=-2\end{cases}$,
∴一次函数的解析式为 $y=-x - 2$;
(2)将 $y = 0$ 代入 $y=-x - 2$,得 $x=-2$, 即直线 $y=-x - 2$ 与 $x$ 轴交于点 $C(-2,0)$,
∴ $S_{\triangle AOB}=S_{\triangle AOC}+S_{\triangle BOC}=\frac{1}{2}\times2\times2+\frac{1}{2}\times2\times4 = 6$, 即 $\triangle AOB$ 的面积是 $6$;
(3)由图可得,不等式 $kx + b-\frac{m}{x}<0$ 的解集为 $x>2$,或 $-4<x<0$。
14. 如图,点$A(1,\frac{1}{2}m^2)$,点$B(2,m - 1)$是函数$y = \frac{k}{x}$(其中$x > 0$)图象上的两点.
(1)求点$A$,点$B$的坐标及函数的解析式;
(2)连接$OA$,$OB$,$AB$,求$\triangle AOB$的面积.

(1)求点$A$,点$B$的坐标及函数的解析式;
(2)连接$OA$,$OB$,$AB$,求$\triangle AOB$的面积.

答案:
解:
(1)
∵点 $A(1,\frac{1}{2}m^{2})$,点 $B(2,m - 1)$ 是函数 $y=\frac{k}{x}$ 图象上的两点,
∴ $k=\frac{1}{2}m^{2}=2(m - 1)$, 解得 $m = 2$,$k = 2$,
∴ $A(1,2)$,$B(2,1)$, 函数的解析式为 $y=\frac{2}{x}$;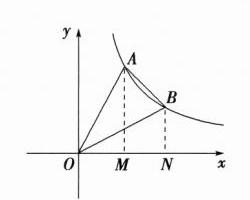
(2)过点 $A$ 作 $AM\perp x$ 轴于 $M$,过点 $B$ 作 $BN\perp x$ 轴于 $N$, $S_{\triangle AOB}=S_{\triangle AOM}+S_{梯形AMNB}-S_{\triangle BON}=S_{梯形AMNB}=\frac{1}{2}\times(2 + 1)\times(2 - 1)=\frac{3}{2}$。
解:
(1)
∵点 $A(1,\frac{1}{2}m^{2})$,点 $B(2,m - 1)$ 是函数 $y=\frac{k}{x}$ 图象上的两点,
∴ $k=\frac{1}{2}m^{2}=2(m - 1)$, 解得 $m = 2$,$k = 2$,
∴ $A(1,2)$,$B(2,1)$, 函数的解析式为 $y=\frac{2}{x}$;

(2)过点 $A$ 作 $AM\perp x$ 轴于 $M$,过点 $B$ 作 $BN\perp x$ 轴于 $N$, $S_{\triangle AOB}=S_{\triangle AOM}+S_{梯形AMNB}-S_{\triangle BON}=S_{梯形AMNB}=\frac{1}{2}\times(2 + 1)\times(2 - 1)=\frac{3}{2}$。
查看更多完整答案,请扫码查看


