《2025年一飞冲天同步训练九年级数学下册人教版》

16. 一块材料的形状是锐角三角形ABC，边BC = 120 mm，高AD = 80 mm，把它加工成正方形零件，如图1，使正方形的一边在BC上，其余两个顶点分别在AB，AC上.
(1)求证：△AEF∽△ABC；
(2)求这个正方形零件的边长；
(3)如果把它加工成矩形零件，如图2，问这个矩形零件的最大面积是多少?

答案： 解：
(1)证明：
∵四边形EGHF为正方形，
∴EF//GH，
∴BC//EF，
∴△AEF∽△ABC；
(2)
∵四边形EGHF为正方形，
∴KD = EF，AK = 80 - KD，
∵△AEF∽△ABC，AD⊥BC，
∴$\frac{EF}{BC}=\frac{AK}{AD}$，即$\frac{KD}{120}=\frac{80 - KD}{80}$， 解得KD = 48.
∴正方形零件的边长为48 mm；
(3)设EF = x，EG = y，
∵△AEF∽△ABC，
∴$\frac{EF}{BC}=\frac{AK}{AD}$，
∴$\frac{x}{120}=\frac{80 - y}{80}$，
∴y = 80 - $\frac{2}{3}x$，
∴矩形面积S = xy = - $\frac{2}{3}x² + 80x = - \frac{2}{3}(x - 60)² + 2400(0 ＜ x ＜ 120)$， 故当x = 60时，此时矩形零件的面积最大，最大面积为2400 mm²。

17. 小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关. 因此，他们认为：可以借助物体的影子长度计算光源到物体的位置. 于是，他们做了以下尝试.
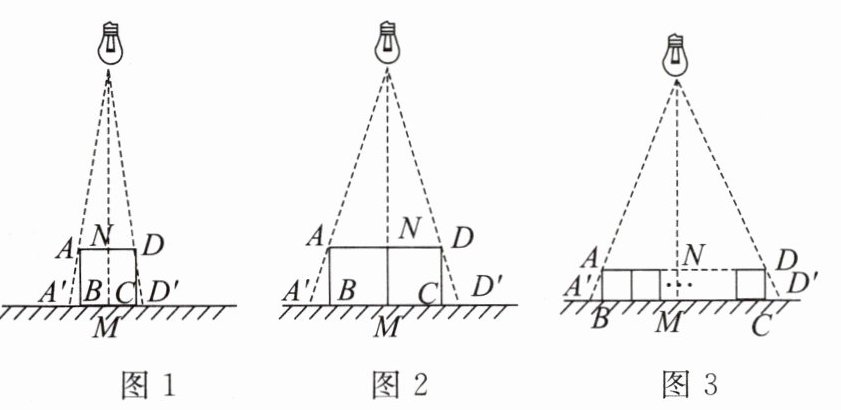
(1)如图1，垂直于地面放置的正方形框架ABCD，边长AB为30 cm，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子A'B，D'C的长度和为6 cm，那么灯泡离地面的高度为_______；
(2)不改变图1中灯泡的高度，将两个边长为30 cm的正方形框架按图2摆放，请计算此时横向影子A'B，D'C的长度和为多少；
(3)有n个边长为a的正方形框架按图3摆放，测得横向影子A'B，D'C的长度和为b，求灯泡离地面的距离.（写出解题过程，结果用含a，b，n的代数式表示）

答案：
解：
(1)180 cm；
(2)记灯泡为点P，如图2. 设横向影子A′B，D′C的长度和为y cm，
∵AD//A′D′，
∴△PAD∽△PA′D′.
∴$\frac{AD}{A′D′}=\frac{PN}{PM}$，即$\frac{60}{60 + y}=\frac{180 - 30}{180}$， 解得y = 12(cm)；
∴此时横向影子A′B，D′C的长度和为12 cm；
(3)记灯泡为点P，如图3.
∵AD//A′D′，
∴△PAD∽△PA′D′.
∴$\frac{AD}{A′D′}=\frac{PN}{PM}$， 设灯泡离地面距离为x， 由题意，得PM = x，PN = x - a，AD = na，A′D′ = na + b，
∴$\frac{na}{na + b}=\frac{x - a}{x}$， 解得x = $\frac{na² + ab}{b}$，
∴灯泡离地面的距离为$\frac{na² + ab}{b}$。