《2025年一飞冲天同步训练九年级数学下册人教版》

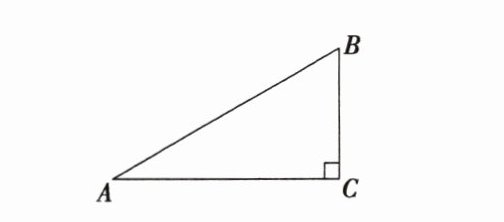
14. 如图，在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$\frac{BC}{AC}=\frac{\sqrt{3}}{3}$，则下列结论中正确的是（ ）


A. $\sin A=\frac{\sqrt{3}}{2}$
B. $\sin B=\frac{1}{2}$
C. $\cos A=\frac{1}{2}$
D. $\tan B=\sqrt{3}$

答案： D $\because\frac{BC}{AC}=\tan A=\frac{\sqrt{3}}{3}$，$\therefore\angle A = 30^{\circ}$，$\therefore\angle B = 60^{\circ}$，$\therefore\sin A=\sin30^{\circ}=\frac{1}{2}$，故A错误；$\therefore\sin B=\sin60^{\circ}=\frac{\sqrt{3}}{2}$，故B错误；$\therefore\cos A=\cos30^{\circ}=\frac{\sqrt{3}}{2}$，故C错误；$\therefore\tan B=\tan60^{\circ}=\sqrt{3}$，故D正确。

15. 已知$\alpha$是锐角，$\sin\alpha=\cos60^{\circ}$，则$\alpha$等于（ ）
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. 不能确定

答案： A $\because\sin\alpha=\cos60^{\circ}=\frac{1}{2}$，$\therefore\alpha = 30^{\circ}$。

16. $\triangle ABC$中，$\angle A,\angle B$均为锐角，且$(\tan B - \sqrt{3})(2\sin A - \sqrt{3}) = 0$，则$\triangle ABC$一定是（ ）
A. 等腰三角形
B. 等边三角形
C. 直角三角形
D. 有一个角是$60^{\circ}$的三角形

答案： D $\because\triangle ABC$中，$\angle A$，$\angle B$均为锐角，且$(\tan B-\sqrt{3})(2\sin A-\sqrt{3}) = 0$，$\therefore\tan B-\sqrt{3}=0$，或$2\sin A-\sqrt{3}=0$，即$\tan B=\sqrt{3}$，或$\sin A=\frac{\sqrt{3}}{2}$。$\therefore\angle B = 60^{\circ}$，或$\angle A = 60^{\circ}$。$\therefore\triangle ABC$是有一个角是$60^{\circ}$的三角形。

17. 在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$AB = 2$，$BC = \sqrt{3}$，则$\sin\frac{A}{2}=$_______.

答案： $\frac{1}{2}$ $\because\sin A=\frac{BC}{AB}=\frac{\sqrt{3}}{2}$，$\therefore\angle A = 60^{\circ}$，$\therefore\sin\frac{A}{2}=\sin30^{\circ}=\frac{1}{2}$。

18. 用计算器比较大小：$\frac{\sqrt{5}-1}{2}$_______$\sin37.5^{\circ}$.

答案： $＞$ $\because\frac{\sqrt{5}-1}{2}\approx0.6180$，$\sin37.5^{\circ}\approx0.6088$，$\therefore\frac{\sqrt{5}-1}{2}＞\sin37.5^{\circ}$。

19. 在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，如果$3BC = \sqrt{3}AC$，那么$\sin A=$_______.

答案： $\frac{1}{2}$ $\because\angle C = 90^{\circ}$，$3BC=\sqrt{3}AC$，$\therefore\tan A=\frac{BC}{AC}=\frac{\sqrt{3}}{3}$，$\therefore\angle A = 30^{\circ}$，$\therefore\sin A=\sin30^{\circ}=\frac{1}{2}$。

20. 若$\alpha,\beta$均为锐角，且$\vert\sin\alpha - \frac{1}{2}\vert+(\sqrt{3}-\tan\beta)^{2}=0$，则$\alpha+\beta=$_______.

答案： $90^{\circ}$ $\because|\sin\alpha-\frac{1}{2}|+(\sqrt{3}-\tan\beta)^{2}=0$，$\therefore\sin\alpha-\frac{1}{2}=0$，$\sqrt{3}-\tan\beta=0$，$\therefore\sin\alpha=\frac{1}{2}$，$\tan\beta=\sqrt{3}$，$\therefore\alpha = 30^{\circ}$，$\beta = 60^{\circ}$，$\therefore\alpha+\beta = 90^{\circ}$。

21. 规定：$\sin(-x)=-\sin x,\cos(-x)=\cos x,\sin(x + y)=\sin x\cos y+\cos x\sin y$. 据此判断下列等式成立的是___________（填序号）.
①$\cos(-60^{\circ})=-\cos60^{\circ}=\frac{1}{2}$；
②$\sin75^{\circ}=\sin(30^{\circ}+45^{\circ})=\sin30^{\circ}\cos45^{\circ}+\cos30^{\circ}\sin45^{\circ}=\frac{\sqrt{2}+\sqrt{6}}{4}$；
③$\sin2x=\sin(x + x)=\sin x\cos x+\cos x\sin x = 2\sin x\cos x$；
④$\sin(x - y)=\sin x\cos y-\cos x\sin y$.

答案： ②③④ $\cos(-60^{\circ})=\cos60^{\circ}=\frac{1}{2}$，故①不成立； $\sin75^{\circ}=\sin(30^{\circ}+45^{\circ})=\sin30^{\circ}\cos45^{\circ}+\cos30^{\circ}\sin45^{\circ}=\frac{\sqrt{6}+\sqrt{2}}{4}$，故②成立； $\sin2x=\sin(x + x)=\sin x\cos x+\cos x\sin x = 2\sin x\cos x$，故③成立； $\sin(x - y)=\sin[x+(-y)]=\sin x\cos(-y)+\cos x\sin(-y)=\sin x\cos y-\cos x\sin y$，故④成立。

22. 计算：
（1）$2\sin60^{\circ}\tan45^{\circ}+4\cos^{2}30^{\circ}-\tan60^{\circ}$；
（2）$\vert2-\tan60^{\circ}\vert-(\pi - 3.14)^{0}+(-\frac{1}{2})^{-2}+\frac{\sqrt{12}}{2}$；
（3）$\frac{\sqrt{2}}{4}\sin45^{\circ}+\cos^{2}30^{\circ}-\frac{1}{2\tan60^{\circ}}+2\sin60^{\circ}$；
（4）$\frac{\sin45^{\circ}+\cos30^{\circ}}{3 - 2\cos60^{\circ}}-\sin60^{\circ}\times(1-\sin30^{\circ})$.

答案： 解：
(1)原式$=2\times\frac{\sqrt{3}}{2}\times1 + 4\times(\frac{\sqrt{3}}{2})^{2}-\sqrt{3}=\sqrt{3}+3-\sqrt{3}=3$；
(2)原式$=|2-\sqrt{3}|-1 + 4+\sqrt{3}=2-\sqrt{3}+3+\sqrt{3}=5$；
(3)原式$=\frac{\sqrt{2}}{4}\times\frac{\sqrt{2}}{2}+(\frac{\sqrt{3}}{2})^{2}-\frac{1}{2\times\sqrt{3}}+2\times\frac{\sqrt{3}}{2}=\frac{1}{4}+\frac{3}{4}-\frac{\sqrt{3}}{6}+\sqrt{3}=1+\frac{5\sqrt{3}}{6}$；
(4)原式$=\frac{\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}}{3 - 2\times\frac{1}{2}}-\frac{\sqrt{3}}{2}\times(1-\frac{1}{2})=\frac{\sqrt{2}+\sqrt{3}}{4}-\frac{\sqrt{3}}{2}\times\frac{1}{2}=\frac{\sqrt{2}}{4}$。