《2025年一飞冲天同步训练九年级数学下册人教版》

1. 关于反比例函数$y = \frac{6}{x}$，下列说法错误的是（ ）
A. 图象经过点(2,3)
B. 图象位于第二、四象限
C. 图象关于原点对称
D. 图象与坐标轴没有交点

答案： B 当 $x = 2$ 时，$y=\frac{6}{2}=3$，
∴函数图象经过点 $(2,3)$，故 A 正确；
∵ $k = 6＞0$，
∴函数图象位于第一、三象限，故 B 错误； 反比例函数 $y=\frac{6}{x}$ 的图象关于原点对称，与坐标轴没有交点，故 C，D 正确。

2. 已知反比例函数$y = \frac{6}{x}$，当$1 ＜ x ＜ 3$时，$y$的取值范围是（ ）
A. $0 ＜ y ＜ 1$
B. $1 ＜ y ＜ 2$
C. $2 ＜ y ＜ 6$
D. $y ＞ 6$

答案： C
∵ $k = 6＞0$，
∴在第一、三象限内，$y$ 随 $x$ 的增大而减小， 又
∵当 $x = 1$ 时，$y = 6$；当 $x = 3$ 时，$y = 2$，
∴当 $1＜x＜3$ 时，$2＜y＜6$。

3. 在反比例函数$y = \frac{k - 2}{x}$图象的每一条曲线上，$y$都随$x$的增大而增大，则$k$的取值范围是（ ）
A. $k ＞ 2$
B. $k ＞ 0$
C. $k \geq 2$
D. $k ＜ 2$

答案： D
∵在反比例函数 $y=\frac{k - 2}{x}$ 图象的每一条曲线上，$y$ 都随 $x$ 的增大而增大，
∴ $k - 2＜0$，
∴ $k＜2$。

4. 在平面直角坐标系中，若点$(-2,y_1)$，$(-1,y_2)$，$(1,y_3)$都在反比例函数$y = - \frac{4}{x}$的图象上，则$y_1$，$y_2$，$y_3$的大小关系是（ ）
A. $y_3 ＜ y_1 ＜ y_2$
B. $y_3 ＜ y_2 ＜ y_1$
C. $y_1 ＜ y_2 ＜ y_3$
D. $y_1 ＜ y_3 ＜ y_2$

答案： A
∵ $k=-4＜0$，
∴在每一个象限内，$y$ 随 $x$ 的增大而增大。
∵ $-2＜-1＜0$，
∴ $y_{2}＞y_{1}＞0$，
∵ $1＞0$，
∴ $y_{3}＜0$，
∴ $y_{3}＜y_{1}＜y_{2}$。

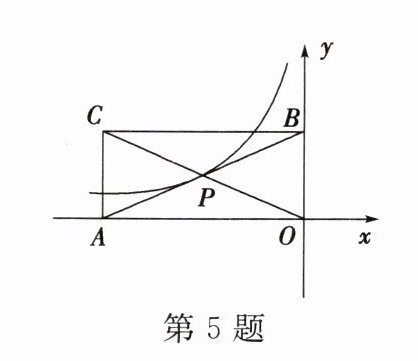
5. 如图，矩形$AOBC$的面积为4，反比例函数$y = \frac{k}{x}(k \neq 0)$的图象的一支经过矩形对角线的交点$P$，则该反比例函数的解析式是（ ）

A. $y = \frac{4}{x}$
B. $y = \frac{2}{x}$
C. $y = - \frac{2}{x}$
D. $y = - \frac{1}{x}$

答案：
D 如图，过点 $P$ 作 $PE\perp x$ 轴于 $E$，$PF\perp y$ 轴于 $F$。$AOBC$ 为矩形，点 $P$ 为对角线的交点，
∴ $S_{矩形OEPF}=\frac{1}{4}S_{矩形AOBC}=\frac{1}{4}\times4 = 1$。
∴ $k=-1$， 故该反比例函数的解析式是 $y=-\frac{1}{x}$。

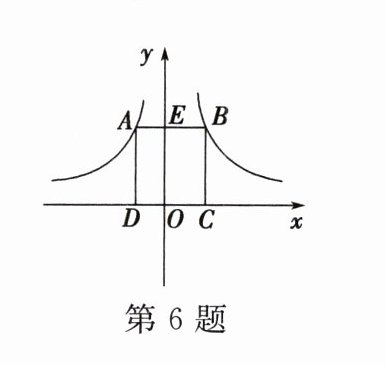
6. 如图，反比例函数$y = \frac{a}{x}$与$y = \frac{b}{x}$的图象上分别有一点$A$，$B$，且$AB // x$轴，$AD \perp x$轴于$D$，$BC \perp x$轴于$C$，若矩形$ABCD$的面积为8，则$b - a =$（ ）

A. 8
B. -8
C. 4
D. -4

答案： A
∵ $AB// x$ 轴，$AD\perp x$ 轴于 $D$，$BC\perp x$ 轴于 $C$，
∴ $|a|=S_{矩形ADOE}$，$|b|=S_{矩形BCOE}$，
∵矩形 $ABCD$ 的面积为 $8$，
∴ $S_{矩形ADOE}+S_{矩形BCOE}=S_{矩形ABCD}=8$，
∴ $|a|+|b|=8$，
∵反比例函数 $y=\frac{a}{x}$ 的图象在第二象限，反比例函数 $y=\frac{b}{x}$ 的图象在第一象限，
∴ $a＜0$，$b＞0$，
∴ $b - a=8$。

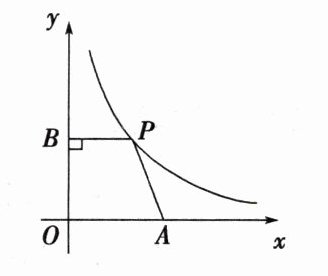
7. 如图，在平面直角坐标系中，点$A$是$x$轴正半轴上的一个定点，点$P$是双曲线$y = \frac{3}{x}(x ＞ 0)$上的一个动点，$PB \perp y$轴于点$B$，当点$P$的横坐标逐渐增大时，四边形$OAPB$的面积将会（ ）


A. 逐渐增大
B. 不变
C. 逐渐减小
D. 先增大后减小

答案： C 设点 $P$ 的坐标为 $(x,\frac{3}{x})$，
∵ $PB\perp y$ 轴于点 $B$，点 $A$ 是 $x$ 轴正半轴上的一个定点，
∴四边形 $OAPB$ 是直角梯形，
∴ $S_{四边形OAPB}=\frac{1}{2}(PB + AO)\cdot BO=\frac{1}{2}(x + AO)\cdot\frac{3}{x}=\frac{3}{2}+\frac{3AO}{2}\cdot\frac{1}{x}$，
∵ $AO$ 是定值，
∴当 $x$ 逐渐增大时，$\frac{1}{x}$ 逐渐减小， 即点 $P$ 的横坐标逐渐增大时，四边形 $OAPB$ 的面积逐渐减小。

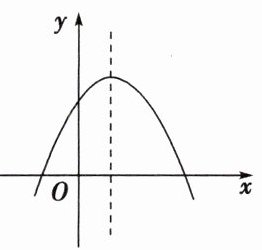
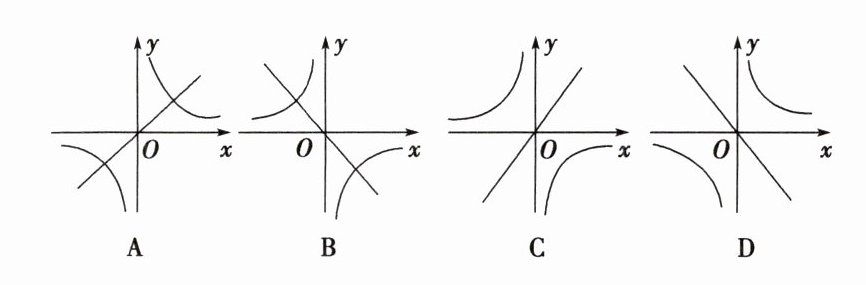
8. 二次函数$y = ax^2 + bx + c$的图象如图所示，反比例函数$y = \frac{a}{x}$与正比例函数$y = cx$在同一坐标系内的大致图象是（ ）

答案： C 由二次函数的图象得 $a＜0$，$c＞0$，
∴反比例函数 $y=\frac{a}{x}$ 的图象在第二、四象限， 正比例函数 $y = cx$ 的图象经过第一、三象限，
∴C 选项正确。