《2025年一飞冲天同步训练九年级数学下册人教版》

1. 在Rt△ABC中，∠C = 90°，则$\frac{BC}{AC}$是∠A的 （ ）
A. 正弦
B. 余弦
C. 正切
D. 以上都不对

答案： C

2. 在△ABC中，∠A = 90°，∠A，∠B，∠C的对边分别为a，b，c，则下列选项中不正确的是 （ ）
A. $\sin B=\frac{b}{a}$
B. $\sin C=\frac{c}{a}$
C. $\cos B=\frac{b}{c}$
D. $\tan B=\frac{b}{c}$

答案： C 因为∠A = 90°，∠A，∠B，∠C的对边分别为a，b，c， 所以sin B = $\frac{b}{a}$，故A正确； 所以sin C = $\frac{c}{a}$，故B正确； 所以cos B = $\frac{c}{a}$，故C不正确； 所以tan B = $\frac{b}{c}$，故D正确。

3. 在△ABC中，∠C = 90°，BC = 3，$\tan A=\frac{3}{4}$，则边AB的长是 （ ）
A. $\sqrt{7}$
B. 3
C. 4
D. 5

答案： D 因为tan A = $\frac{BC}{AC}$ = $\frac{3}{4}$，BC = 3，所以AC = 4， 由勾股定理得AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{4^{2}+3^{2}}$ = 5。

4. 在Rt△ABC中，∠C = 90°，AC = 1，BC = 2，则$\tan A$的值为 （ ）
A. 2
B. $\frac{1}{2}$
C. $\frac{\sqrt{5}}{5}$
D. $\frac{2\sqrt{5}}{5}$

答案： A 因为∠C = 90°，AC = 1，BC = 2， 所以tan A = $\frac{BC}{AC}$ = $\frac{2}{1}$ = 2。

5. 在Rt△ABC中，∠C = 90°，AC = 5，BC = 12，则$\cos B$的值为 （ ）
A. $\frac{5}{13}$
B. $\frac{12}{13}$
C. $\frac{13}{5}$
D. $\frac{5}{12}$

答案： B 由勾股定理得AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{5^{2}+12^{2}}$ = 13， 则cos B = $\frac{BC}{AB}$ = $\frac{12}{13}$。

6. 在△ABC中，∠C = 90°，$\tan A=\frac{\sqrt{3}}{3}$，则$\cos B=$ （ ）
A. $\frac{\sqrt{3}}{2}$
B. $\frac{1}{2}$
C. $\frac{\sqrt{3}}{3}$
D. $\sqrt{3}$

答案： B 因为∠C = 90°，所以tan A = $\frac{BC}{AC}$ = $\frac{\sqrt{3}}{3}$， 设BC = $\sqrt{3}x$，AC = 3x， 由勾股定理得 AB = $\sqrt{BC^{2}+AC^{2}}$ = $\sqrt{(\sqrt{3}x)^{2}+(3x)^{2}}$ = 2$\sqrt{3}x$， 所以cos B = $\frac{BC}{AB}$ = $\frac{\sqrt{3}x}{2\sqrt{3}x}$ = $\frac{1}{2}$。

7. 如图，过∠MAN的边AM上的一点B（不与点A重合）作BC⊥AN于点C，过点C作CD⊥AM于点D，则下列线段的比等于$\tan A$的是 （ ）


A. $\frac{CD}{AC}$
B. $\frac{BD}{BC}$
C. $\frac{BD}{CD}$
D. $\frac{CD}{BC}$

答案： C 因为BC⊥AN， 所以∠ABC + ∠A = 90°， 因为CD⊥AM， 所以∠ABC + ∠DCB = 90°， 所以∠A = ∠DCB， 所以tan A = tan∠DCB = $\frac{BD}{CD}$。

8. 在直角三角形ABC中，若2AB = AC，则$\cos C=$ __________.

答案： $\frac{\sqrt{3}}{2}$或$\frac{2\sqrt{5}}{5}$ 若∠B = 90°，设AB = x，则AC = 2x， 所以BC = $\sqrt{AC^{2}-AB^{2}}$ = $\sqrt{(2x)^{2}-x^{2}}$ = $\sqrt{3}x$， 所以cos C = $\frac{BC}{AC}$ = $\frac{\sqrt{3}x}{2x}$ = $\frac{\sqrt{3}}{2}$； 若∠A = 90°， 设AB = x，则AC = 2x， 所以BC = $\sqrt{AC^{2}+AB^{2}}$ = $\sqrt{(2x)^{2}+x^{2}}$ = $\sqrt{5}x$， 所以cos C = $\frac{AC}{BC}$ = $\frac{2x}{\sqrt{5}x}$ = $\frac{2\sqrt{5}}{5}$； 综上所述，cos C的值为$\frac{\sqrt{3}}{2}$或$\frac{2\sqrt{5}}{5}$。

9. 在锐角△ABC中，AB = 15，BC = 14，$S_{\triangle ABC}=84$，求：
（1）$\tan C$的值；
（2）$\sin A$的值.

答案：
解：
(1)如图，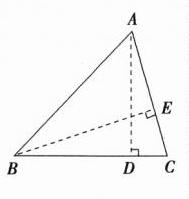
过点A作AD⊥BC于点D。 因为$S_{\triangle ABC}$ = $\frac{1}{2}BC\cdot AD$ = 84， 所以$\frac{1}{2}\times14\times AD$ = 84， 所以AD = 12。 又因为AB = 15， 所以BD = $\sqrt{AB^{2}-AD^{2}}$ = 9。 所以CD = 14 - 9 = 5。 所以tan C = $\frac{AD}{CD}$ = $\frac{12}{5}$；
(2)如图，过点B作BE⊥AC于点E。 在Rt△ADC中，AC = $\sqrt{AD^{2}+DC^{2}}$ = 13， 因为$S_{\triangle ABC}$ = $\frac{1}{2}AC\cdot BE$ = 84， 所以$\frac{1}{2}\times13\times BE$ = 84， 所以BE = $\frac{168}{13}$， 所以sin A = $\frac{BE}{AB}$ = $\frac{\frac{168}{13}}{15}$ = $\frac{56}{65}$。

10. 在Rt△ABC中，∠ACB = 90°.
（1）$\tan A$与$\sin A$，$\cos A$之间有什么关系？并说明理由；
（2）若$\frac{\sin^{2}A - \sin A\cos A}{\cos^{2}A + \sin A\cos A}=\frac{2}{3}$，求$\tan A$的值.

答案： 解：
(1)tan A = $\frac{\sin A}{\cos A}$。理由如下： 记∠A，∠B，∠C的对边分别为a，b，c，则tan A = $\frac{a}{b}$，sin A = $\frac{a}{c}$，cos A = $\frac{b}{c}$， 因为$\frac{\sin A}{\cos A}$ = $\frac{a}{c}\times\frac{c}{b}$ = $\frac{a}{b}$， 所以tan A = $\frac{\sin A}{\cos A}$；
(2)分式的分子、分母同时除以$\cos^{2}A$得： 原式 = $\frac{\tan^{2}A - \tan A}{1 + \tan A}$ = $\frac{2}{3}$。 整理得3$\tan^{2}A$ - 5tan A - 2 = 0。 解得tan A = 2，或tan A = - $\frac{1}{3}$（舍去）。 所以tan A的值为2。