《2025年一飞冲天同步训练九年级数学下册人教版》

7. 一座楼梯的示意图如图所示，BC 是铅垂线，AC 是水平线，BA 与 AC 的夹角为θ. 现要在楼梯上铺一条地毯，已知 AC = 4 m，楼梯宽度为 1 m，则地毯的面积至少需要（ ）

A. $\frac{4}{\sin \theta}$ m² B. $\frac{4}{\cos \theta}$ m²
C. $(4 + \frac{4}{\tan \theta})$m² D. (4 + 4tan θ)m²

答案： D 在Rt△ABC中，BC = AC·tanθ = 4tanθ，所以AC + BC = 4 + 4tanθ，所以地毯的面积至少需要1×(4 + 4tanθ) = (4 + 4tanθ)m²。

8. 如图，一个直角梯形的堤坝坡长 AB 为 6 米，斜坡 AB 的坡角为 60°，为了改善堤坝的稳固性，准备将其坡角改为 45°，则调整后的斜坡 AE 的长度为（ ）

A. 3$\sqrt{6}$米 B. 3$\sqrt{3}$米
C. (3$\sqrt{3}$ - 2)米 D. (3$\sqrt{3}$ - 3)米

答案：
A 如图，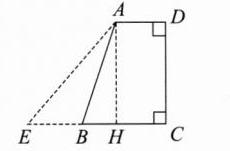
作AH⊥BC于H。在Rt△ABH中，sin∠ABH = AH/AB，则AH = AB·sin∠ABH = 6×sin60° = 6×√3/2 = 3√3，因为∠E = 45°，所以AE = √2AH = √2×3√3 = 3√6（米）。

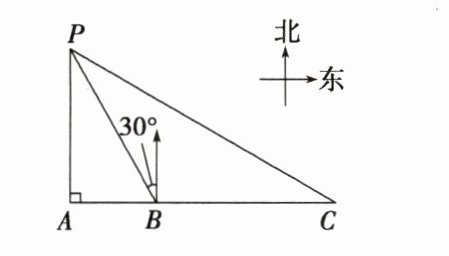
9. 如图，某海监船以 20 km/h 的速度在某海域执行巡航任务，当海监船由西向东航行至 A 处时，测得岛屿 P 恰好在其正北方向，继续向东航行 1 小时到达 B 处，这时，测得岛屿 P 在其北偏西 30°方向，则海监船到岛屿的最小距离是______km；保持航向不变，又航行 2 小时到达 C 处，此时海监船与岛屿 P 之间的距离（即 PC 的长）为______km（结果保留根号）.

答案： 20√3 40√3 在Rt△PAB中，AB = 20，∠APB = 30°，所以PB = 2AB = 40，PA = AB/tan∠APB = 20/tan30° = 20√3，所以海监船到岛屿的最小距离是20√3 km；由题意BC = 40，所以PB = BC，所以∠C = ∠CPB，因为∠ABP = ∠C + ∠CPB = 60°，所以∠C = 30°，所以PC = 2PA = 2×20√3 = 40√3(km)。即海监船到达C处时与岛屿P之间的距离为40√3 km。

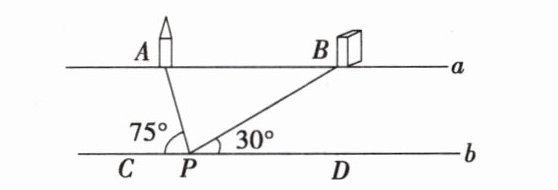
10. 如图，河流两岸 a，b 互相平行，点 A，B 是河岸 a 上的两座建筑物，点 C，D 是河岸 b 上的两点，A，B 的距离约为 200 米. 某人在河岸 b 上的点 P 处测得∠APC = 75°，∠BPD = 30°，则河流的宽度约为______米.

答案：
100 如图，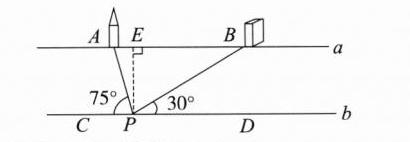
过点P作PE⊥AB于点E。因为∠APC = 75°，∠BPD = 30°，所以∠APB = 75°，因为∠BAP = ∠APC = 75°，所以∠APB = ∠BAP，所以AB = PB = 200，因为∠ABP = ∠BPD = 30°，所以PE = 1/2PB = 100米，即河流的宽度约为100米。

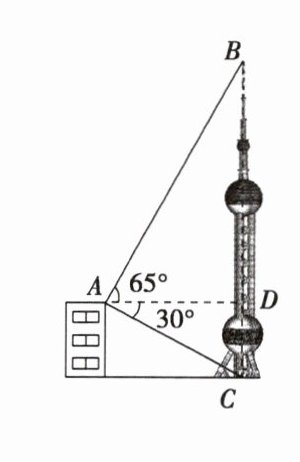
11. 某数学兴趣小组想测量电视塔的高度，如图，该小组在电视塔 BC 前的一座楼房楼顶 A 处观测到电视塔最高点 B 的仰角为 65°，电视塔最低点 C 的俯角为 30°，楼顶 A 与电视塔的水平距离 AD 为 90 米，求电视塔 BC 的高度.（结果精确到 1 米，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，sin 65°≈0.91，cos 65°≈0.42，tan 65°≈2.14）

答案： 解：在Rt△ADB中，因为∠BAD = 65°，AD = 90，所以BD = AD·tan65°≈90×2.14 = 192.6，同理，在Rt△ADC中，因为∠DAC = 30°，AD = 90，所以CD = AD·tan30° = 90×√3/3≈51.9。所以BC = BD + CD = 192.6 + 51.9 = 244.5≈245（米）。所以电视塔BC的高度约为245米。