《2025年一飞冲天同步训练九年级数学下册人教版》

1. 函数$y = 3x^{-1}$是（ ）
A. 正比例函数
B. 一次函数
C. 反比例函数
D. 二次函数

答案： C

2. 下列函数中是反比例函数的是（ ）
A. $y = -x + 1$
B. $y = -2x^{-1}$
C. $y = -\frac{x}{2}$
D. $y = x^{2} + 5$

答案： B

3. 已知点$A(2,m + 1)$在反比例函数$y = -\frac{12}{x}$的图象上，则$m =$_______.

答案： -7 因为点A(2, m + 1)在反比例函数y = -$\frac{12}{x}$的图象上，所以m + 1 = -$\frac{12}{2}$，解得m = -7。

4. 若$a$与$b$成反比例，则$m =$_______.

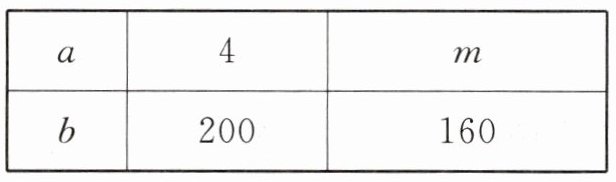
答案： 5 因为a与b成反比例，所以ab = 4×200 = 160m，所以m = 5。

5. 请指出下面哪些图中的$y$与$x$符合反比例函数关系.

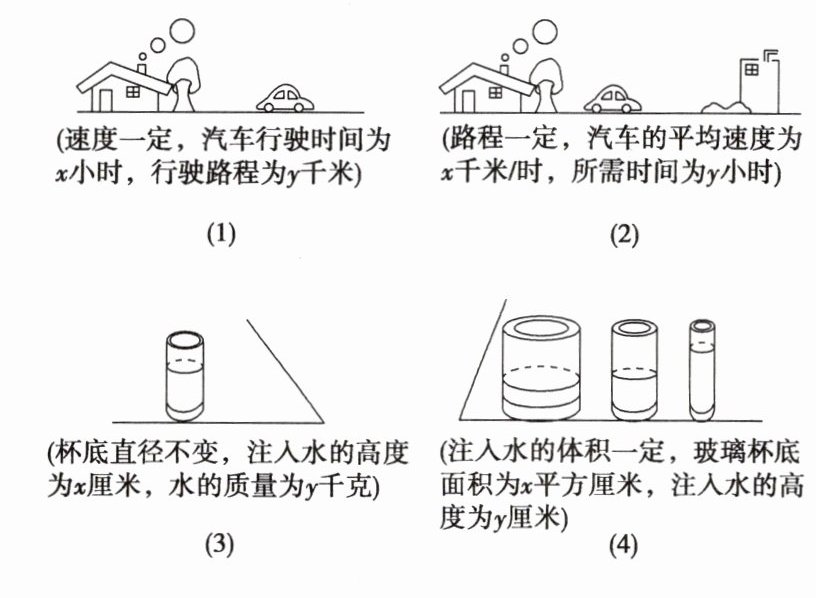
答案： 解：图中函数关系式分别是 （1）y = vx（v表示速度）是正比例函数； （2）y = $\frac{s}{x}$（s表示路程）是反比例函数； （3）y = kx（k为底面直径一定时单位高度水的质量）是正比例函数； （4）y = $\frac{V}{x}$（V表示水的体积）是反比例函数； 故图（2）和图（4）中的y与x符合反比例函数关系。

6. 在下列函数中，$y$是$x$的反比例函数的是（ ）
A. $y = 3x$
B. $y = \frac{x}{3}$
C. $y = \frac{3}{x}$
D. $y = \frac{3}{x - 1}$

答案： C

7. 下列函数：①$y = x - 2$，②$y = \frac{x}{3}$，③$y = x^{-1}$，④$y = \frac{2}{x + 1}$，$y$是$x$的反比例函数的个数为（ ）
A. 0
B. 1
C. 2
D. 3

答案： B ①y = x - 2，y是x的一次函数； ②y = $\frac{x}{3}$，y是x的正比例函数； ③y = x⁻¹，y是x的反比例函数； ④y = $\frac{2}{x + 1}$，y是x + 1的反比例函数。 综上所述，y是x的反比例函数的个数为1。

8. 若函数$y = (m + 1)x^{|m| - 2}$是反比例函数，则$m =$（ ）
A. $\pm1$
B. $\pm3$
C. $-1$
D. 1

答案： D 因为函数y = (m + 1)x^(|m| - 2)是反比例函数，所以|m| - 2 = -1，且m + 1 ≠ 0，解得m = ±1，且m ≠ -1，所以m = 1。

9. 已知$y$与$x$成反比例，且当$x = 2$时，$y = 3$，则该函数解析式是（ ）
A. $y = 6x$
B. $y = \frac{x}{3}$
C. $y = \frac{6}{x}$
D. $y = \frac{6}{x^{-1}}$

答案： C 设y = $\frac{k}{x}$，则3 = $\frac{k}{2}$，解得k = 6，所以该函数解析式是y = $\frac{6}{x}$。

10. 如果一个等腰三角形的面积为 10，底边长为$x$，底边上的高为$y$，则$y$与$x$的函数解析式为（ ）
A. $y = \frac{10}{x}$
B. $y = \frac{5}{x}$
C. $y = \frac{20}{x}$
D. $y = \frac{x}{20}$

答案： C 因为等腰三角形的面积为10，底边长为x，底边上的高为y，所以$\frac{1}{2}$xy = 10，所以y与x的函数解析式为y = $\frac{20}{x}$。