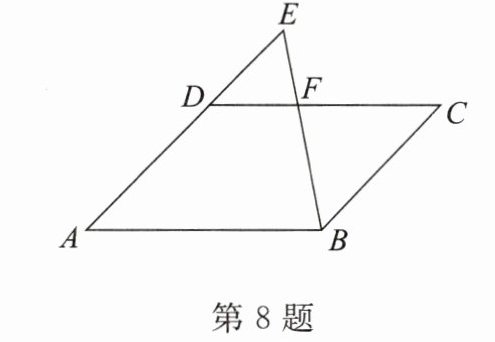
8. 如图,在$\square ABCD$中,$AB = 9$,$AD = 8$,$E$为$AD$延长线上一点,且$DE = 4$,连接$BE$交$CD$于点$F$,则$CF =$__________.

答案:
6 因为四边形ABCD是平行四边形,所以BC = AD = 8,AB = CD = 9,AD//BC,
所以∠BCF = ∠EDF,∠BFC = ∠EFD,所以△BCF∽△EDF,所以$\frac{BC}{ED}=\frac{CF}{DF}$,
即$\frac{8}{4}=\frac{CF}{9 - CF}$,解得CF = 6。
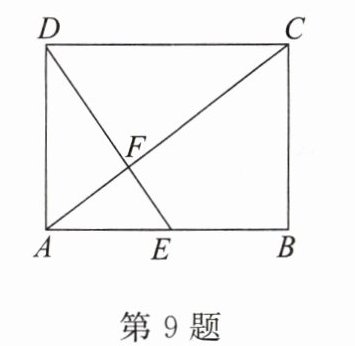
9. 如图,在矩形$ABCD$中,$E$是边$AB$的中点,连接$DE$交对角线$AC$于点$F$,若$AB = 8$,$AD = 6$,则$AF$的长为__________.

答案:
$\frac{10}{3}$ 因为四边形ABCD是矩形,所以AB = CD = 8,∠ADC = 90°,AB//CD,
因为AD = 6,所以AC = $\sqrt{AD^{2}+CD^{2}}=\sqrt{6^{2}+8^{2}} = 10$,
因为E是AB的中点,所以AE = $\frac{1}{2}$AB = 4,
因为AB//CD,所以∠CDF = ∠AEF,∠DCF = ∠EAF,所以△CDF∽△AEF,
所以$\frac{CF}{AF}=\frac{CD}{AE}=\frac{8}{4}=2$,所以AF = $\frac{1}{3}$AC = $\frac{10}{3}$。
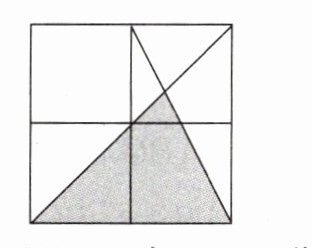
10. 在如图所示的网格中,每个小正方形的边长为1,则阴影部分图形的面积为__________.

答案:
$\frac{4}{3}$ 如图,过点E作EM⊥AB于点M,EN⊥DC于点N, 由题意得,AB = 1,MN = BC = CD = 2,AB//CD,所以∠BAE = ∠DCE,∠ABE = ∠CDE, 所以△ABE∽△CDE,又$\frac{AB}{CD}=\frac{1}{2}$,所以$\frac{EM}{EN}=\frac{1}{2}$,所以EN = $\frac{2}{3}$MN = $\frac{4}{3}$, 所以阴影部分图形的面积为$\frac{1}{2}\times2\times\frac{4}{3}=\frac{4}{3}$。
$\frac{4}{3}$ 如图,过点E作EM⊥AB于点M,EN⊥DC于点N, 由题意得,AB = 1,MN = BC = CD = 2,AB//CD,所以∠BAE = ∠DCE,∠ABE = ∠CDE, 所以△ABE∽△CDE,又$\frac{AB}{CD}=\frac{1}{2}$,所以$\frac{EM}{EN}=\frac{1}{2}$,所以EN = $\frac{2}{3}$MN = $\frac{4}{3}$, 所以阴影部分图形的面积为$\frac{1}{2}\times2\times\frac{4}{3}=\frac{4}{3}$。

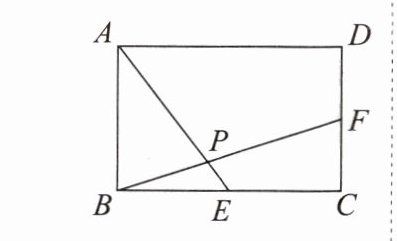
11. 如图,在矩形$ABCD$中,$E$,$F$分别是$BC$,$CD$的中点,$AE$,$BF$交于点$P$.
(1)求证:$AP = 4PE$;
(2)若$\angle BPE=\angle BFD$,且$AD = 8$,求四边形$PFCE$的面积.
(1)求证:$AP = 4PE$;
(2)若$\angle BPE=\angle BFD$,且$AD = 8$,求四边形$PFCE$的面积.

答案:
解:
(1)证明:如图,取BF的中点G,连接EG, 因为E是BC的中点,所以EG是△BCF的中位线,所以EG//CD,CF = 2EG, 因为四边形ABCD是矩形,所以AB//CD,AB = CD,所以EG//AB, 因为F是CD的中点,所以CD = 2CF,所以AB = CD = 2CF = 4EG, 因为EG//AB,所以∠BAP = ∠GEP,∠ABP = ∠EGP,所以△ABP∽△EGP, 所以$\frac{AP}{EP}=\frac{AB}{EG}=4$,所以AP = 4PE;
(2)因为AD = 8,所以BE = $\frac{1}{2}$BC = $\frac{1}{2}$AD = 4。 因为∠BPE = ∠BFD,∠BFD + ∠2 = 180°,∠BPE + ∠1 = 180°,所以∠1 = ∠2, 因为AB//CD,所以∠3 = ∠2,所以∠1 = ∠3,所以AB = AP = 4PE, 设PE = a,则AB = AP = 4a,AE = AP + PE = 5a, 在Rt△ABE中,由勾股定理得$AB^{2}+BE^{2}=AE^{2}$,即$(4a)^{2}+4^{2}=(5a)^{2}$,解得a = $\frac{4}{3}$, 所以AB = $\frac{16}{3}$,CF = $\frac{8}{3}$, 所以$S_{\triangle ABE}=\frac{1}{2}AB\cdot BE=\frac{1}{2}\times\frac{16}{3}\times4=\frac{32}{3}$,$S_{\triangle BCF}=\frac{1}{2}BC\cdot CF=\frac{1}{2}\times8\times\frac{8}{3}=\frac{32}{3}$。 所以$S_{\triangle ABE}=S_{\triangle BCF}$,所以$S_{\triangle ABE}-S_{\triangle BPE}=S_{\triangle BCF}-S_{\triangle BPE}$,所以$S_{\triangle ABP}=S_{四边形PFCE}$, 因为AP = 4PE,所以$S_{\triangle ABP}=\frac{4}{5}S_{\triangle ABE}=\frac{128}{15}$,所以四边形PFCE的面积为$\frac{128}{15}$。
解:
(1)证明:如图,取BF的中点G,连接EG, 因为E是BC的中点,所以EG是△BCF的中位线,所以EG//CD,CF = 2EG, 因为四边形ABCD是矩形,所以AB//CD,AB = CD,所以EG//AB, 因为F是CD的中点,所以CD = 2CF,所以AB = CD = 2CF = 4EG, 因为EG//AB,所以∠BAP = ∠GEP,∠ABP = ∠EGP,所以△ABP∽△EGP, 所以$\frac{AP}{EP}=\frac{AB}{EG}=4$,所以AP = 4PE;
(2)因为AD = 8,所以BE = $\frac{1}{2}$BC = $\frac{1}{2}$AD = 4。 因为∠BPE = ∠BFD,∠BFD + ∠2 = 180°,∠BPE + ∠1 = 180°,所以∠1 = ∠2, 因为AB//CD,所以∠3 = ∠2,所以∠1 = ∠3,所以AB = AP = 4PE, 设PE = a,则AB = AP = 4a,AE = AP + PE = 5a, 在Rt△ABE中,由勾股定理得$AB^{2}+BE^{2}=AE^{2}$,即$(4a)^{2}+4^{2}=(5a)^{2}$,解得a = $\frac{4}{3}$, 所以AB = $\frac{16}{3}$,CF = $\frac{8}{3}$, 所以$S_{\triangle ABE}=\frac{1}{2}AB\cdot BE=\frac{1}{2}\times\frac{16}{3}\times4=\frac{32}{3}$,$S_{\triangle BCF}=\frac{1}{2}BC\cdot CF=\frac{1}{2}\times8\times\frac{8}{3}=\frac{32}{3}$。 所以$S_{\triangle ABE}=S_{\triangle BCF}$,所以$S_{\triangle ABE}-S_{\triangle BPE}=S_{\triangle BCF}-S_{\triangle BPE}$,所以$S_{\triangle ABP}=S_{四边形PFCE}$, 因为AP = 4PE,所以$S_{\triangle ABP}=\frac{4}{5}S_{\triangle ABE}=\frac{128}{15}$,所以四边形PFCE的面积为$\frac{128}{15}$。

1. 如图,在$\triangle ABC$中,点$D$,$E$分别在$AB$,$AC$上,若$\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{3}$,且$\triangle ADE$的面积为9,则四边形$BCED$的面积为 ( )

A. $18$ B. $27$ C. $72$ D. $81$

A. $18$ B. $27$ C. $72$ D. $81$
答案:
1. C 因为\(\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{3}\),\(\angle A = \angle A\),所以\(\triangle ADE\sim\triangle ABC\),所以\(\frac{S_{\triangle ADE}}{S_{\triangle ABC}} = (\frac{1}{3})^2=\frac{1}{9}\),因为\(\triangle ADE\)的面积为9,所以\(\triangle ABC\)的面积为81,所以四边形BCED的面积为81 - 9 = 72。
2. 如图,在$\triangle ABC$中,$CH\perp AB$,$CH = h$,$AB = c$,若内接正方形$DEFG$的边长是$x$,则$h$,$c$,$x$的数量关系为 ( )

A. $x^{2}+h^{2}=c^{2}$ B. $\frac{1}{2}x + h = c$ C. $h^{2}=xc$ D. $\frac{1}{x}=\frac{1}{h}+\frac{1}{c}$

A. $x^{2}+h^{2}=c^{2}$ B. $\frac{1}{2}x + h = c$ C. $h^{2}=xc$ D. $\frac{1}{x}=\frac{1}{h}+\frac{1}{c}$
答案:
2. D 如图,
设CH与GF交于点M,因为四边形DEFG是正方形,\(CH\perp AB\),所以\(GF\parallel DE\),\(GF = EF = MH = x\),所以\(\triangle CGF\sim\triangle CAB\),所以\(\frac{GF}{AB}=\frac{CM}{CH}\),即\(\frac{x}{c}=\frac{h - x}{h}\),所以\(\frac{x}{c}=1-\frac{x}{h}\),所以\(\frac{1}{c}=\frac{1}{x}-\frac{1}{h}\),所以\(\frac{1}{x}=\frac{1}{h}+\frac{1}{c}\)。
2. D 如图,

设CH与GF交于点M,因为四边形DEFG是正方形,\(CH\perp AB\),所以\(GF\parallel DE\),\(GF = EF = MH = x\),所以\(\triangle CGF\sim\triangle CAB\),所以\(\frac{GF}{AB}=\frac{CM}{CH}\),即\(\frac{x}{c}=\frac{h - x}{h}\),所以\(\frac{x}{c}=1-\frac{x}{h}\),所以\(\frac{1}{c}=\frac{1}{x}-\frac{1}{h}\),所以\(\frac{1}{x}=\frac{1}{h}+\frac{1}{c}\)。
3. 如图,网格中的每个小正方形的边长为1,点$A$,$B$都在小正方形的顶点上,线段$AB$与网格线$MN$交于点$C$,则$AC$的长为 ( )

A. $\frac{3}{2}$ B. $\frac{4}{3}$ C. $\frac{5}{4}$ D. $\frac{6}{5}$

A. $\frac{3}{2}$ B. $\frac{4}{3}$ C. $\frac{5}{4}$ D. $\frac{6}{5}$
答案:
3. C 如图,
由题意得\(AB = \sqrt{AD^{2}+BD^{2}}=\sqrt{4^{2}+3^{2}} = 5\),因为\(CN\parallel BD\),所以\(\triangle ANC\sim\triangle ADB\),所以\(\frac{AN}{AD}=\frac{AC}{AB}\),即\(\frac{1}{4}=\frac{AC}{5}\),解得\(AC=\frac{5}{4}\)。
3. C 如图,

由题意得\(AB = \sqrt{AD^{2}+BD^{2}}=\sqrt{4^{2}+3^{2}} = 5\),因为\(CN\parallel BD\),所以\(\triangle ANC\sim\triangle ADB\),所以\(\frac{AN}{AD}=\frac{AC}{AB}\),即\(\frac{1}{4}=\frac{AC}{5}\),解得\(AC=\frac{5}{4}\)。
4. 如图,点$P$是$\triangle ABC$的重心,过点$P$作$PD// BC$,交$AC$于点$D$,连接$PC$,若$\triangle ABC$的面积为1,则$\triangle PDC$的面积为 ( )

A. $\frac{1}{8}$ B. $\frac{1}{9}$ C. $\frac{2}{15}$ D. $\frac{4}{27}$

A. $\frac{1}{8}$ B. $\frac{1}{9}$ C. $\frac{2}{15}$ D. $\frac{4}{27}$
答案:
4. B 如图,
连接AP并延长交BC于点E。因为点P是\(\triangle ABC\)的重心,所以\(BE = EC=\frac{1}{2}BC\),\(\frac{AP}{PE}=2\),所以\(S_{\triangle AEC}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}\),因为\(PD\parallel BC\),所以\(\frac{AP}{PE}=\frac{AD}{DC}=2\),\(\frac{S_{\triangle APD}}{S_{\triangle PDC}} = 2\),因为\(PD\parallel BC\),所以\(\triangle APD\sim\triangle AEC\),所以\(\frac{S_{\triangle APD}}{S_{\triangle AEC}} = (\frac{AP}{AE})^2 = (\frac{2}{3})^2=\frac{4}{9}\),所以\(S_{\triangle APD}=\frac{4}{9}S_{\triangle AEC}=\frac{2}{9}\),所以\(S_{\triangle PDC}=\frac{1}{2}S_{\triangle APD}=\frac{1}{9}\)。
4. B 如图,

连接AP并延长交BC于点E。因为点P是\(\triangle ABC\)的重心,所以\(BE = EC=\frac{1}{2}BC\),\(\frac{AP}{PE}=2\),所以\(S_{\triangle AEC}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}\),因为\(PD\parallel BC\),所以\(\frac{AP}{PE}=\frac{AD}{DC}=2\),\(\frac{S_{\triangle APD}}{S_{\triangle PDC}} = 2\),因为\(PD\parallel BC\),所以\(\triangle APD\sim\triangle AEC\),所以\(\frac{S_{\triangle APD}}{S_{\triangle AEC}} = (\frac{AP}{AE})^2 = (\frac{2}{3})^2=\frac{4}{9}\),所以\(S_{\triangle APD}=\frac{4}{9}S_{\triangle AEC}=\frac{2}{9}\),所以\(S_{\triangle PDC}=\frac{1}{2}S_{\triangle APD}=\frac{1}{9}\)。
查看更多完整答案,请扫码查看


