《2025年一飞冲天同步训练九年级数学下册人教版》

1. 如图，某座山$AB$的顶部有一座通信塔$BC$，且点$A,B,C$在同一条直线上. 从地面$P$处测得塔顶$C$的仰角为$42^{\circ}$，测得塔底$B$的仰角为$35^{\circ}$. 已知通信塔$BC$的高度为$32\ m$，求这座山$AB$的高度(结果取整数).
参考数据：$\tan35^{\circ}\approx0.70,\tan42^{\circ}\approx0.90$.

答案： 解：在Rt△APB中，∠APB = 35°，
∴AB = AP·tan 35°， 在Rt△APC中，∠APC = 42°，
∴AC = AP·tan 42°，
∵AC - AB = BC = 32， AP·tan 42° - AP·tan 35° = 32，
∴AP = $\frac{32}{\tan 42^{\circ}-\tan 35^{\circ}}$，
∴AB = AP·tan 35° = $\frac{32\times\tan 35^{\circ}}{\tan 42^{\circ}-\tan 35^{\circ}}\approx112$(m)，
∴这座山AB的高度约为112 m.

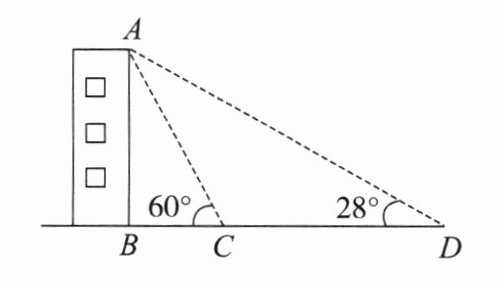
2. 如图，学校数学兴趣小组同学计划测量建筑物$AB$的高度，先在$D$处测得该建筑物顶端$A$的仰角为$28^{\circ}$，然后从$D$处前进$40\ m$到达$C$处，在$C$处测得该建筑物顶端$A$的仰角为$60^{\circ}$，点$B,C,D$在同一条直线上，且$AB\perp CD$. 求建筑物$AB$的高度(结果精确到$0.1\ m$).
参考数据：$\sin28^{\circ}\approx0.47,\cos28^{\circ}\approx0.88,\tan28^{\circ}\approx0.53,\sqrt{3}\approx1.73$.

答案： 解：
∵AB⊥CD，
∴∠ABC = 90°， 在Rt△ABC中，∠ACB = 60°，
∴BC = $\frac{AB}{\tan 60^{\circ}}$， 在Rt△ABD中，∠D = 28°，
∴BD = $\frac{AB}{\tan 28^{\circ}}$.
∵BD - BC = CD = 40，
∴$\frac{AB}{\tan 28^{\circ}}-\frac{AB}{\tan 60^{\circ}} = 40$，
∴AB = $\frac{40\times\tan 28^{\circ}\times\tan 60^{\circ}}{\tan 60^{\circ}-\tan 28^{\circ}}\approx30.6$(m)，
∴建筑物AB的高度约为30.6 m.