《2025年一飞冲天同步训练九年级数学下册人教版》

10. 如图，矩形$ABCD$中，$E$是$CD$延长线上一点，连接$BE$交$AD$于点$F$，连接$CF$，已知$AB = 1$，$BC = 2$，若$\triangle ABF$与$\triangle CEF$的面积相等，则$DE$的长为（ ）


A. 1
B. $\frac{1}{2}$
C. $\frac{\sqrt{2}}{2}$
D. $\frac{\sqrt{5}-1}{2}$

答案： D 设DE = x。因为DF//BC，所以△EFD∽△EBC，所以$\frac{DF}{CB}=\frac{DE}{CE}$，所以$\frac{DF}{2}=\frac{x}{x + 1}$，所以$DF=\frac{2x}{x + 1}$，$AF = 2-\frac{2x}{x + 1}=\frac{2}{x + 1}$。因为△ABF与△CEF的面积相等，所以$\frac{1}{2}\cdot AF\cdot AB=\frac{1}{2}\cdot CE\cdot DF$，所以$\frac{2}{x + 1}\times1=(x + 1)\times\frac{2x}{x + 1}$，整理得$x^2 + x - 1 = 0$，解得$x_1=\frac{\sqrt{5}-1}{2}$，$x_2=\frac{-\sqrt{5}-1}{2}$（舍去），所以DE的长为$\frac{\sqrt{5}-1}{2}$。

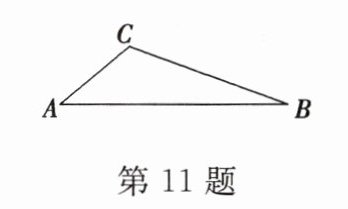
11. 如图，在$\triangle ABC$纸板中，$AC = 4$，$BC = 8$，$AB = 11$，$P$是$BC$上一点，沿过点$P$的直线剪下一个与$\triangle ABC$相似的小三角形纸板，如果有$4$种不同的剪法，那么$CP$长的取值范围是（ ）


A. $0＜CP\leqslant1$
B. $0＜CP\leqslant2$
C. $1\leqslant CP＜8$
D. $2\leqslant CP＜8$

答案：
B 如图所示，过点P作PD//AB交AC于D，或PE//AC交AB于E，
则△DPC∽△ABC，△EBP∽△ABC，此时0 ＜ CP ＜ 8；如图所示，过点P作∠BPF = ∠A交AB于F，
则△PBF∽△ABC，此时0≤CP ＜ 8；如图所示，过点P作∠CPG = ∠A交AC于G，
则△PGC∽△ABC，$\frac{GC}{BC}=\frac{CP}{CA}$，当点G与点A重合时，$AC^2 = CP\cdot BC$，所以$CP=\frac{AC^2}{BC}=\frac{4^2}{8}=2$，所以此时0 ＜ CP≤2。综上所述，CP长的取值范围是0 ＜ CP≤2。

12. 已知$\triangle ABC\sim\triangle DEF$，相似比为$3$，则$\triangle ABC$与$\triangle DEF$的面积之比为________.

答案： 9 因为△ABC与△DEF的相似比为3，所以△ABC与△DEF的面积之比为$3^2 = 9$。

13. 如果把两条直角边长分别为$5$，$10$的直角三角形按相似比$\frac{3}{5}$进行缩小，得到的直角三角形的面积是________.

答案： 9 设缩小后的直角三角形的两条直角边分别为a，b（a ＜ b），根据题意得$\frac{a}{5}=\frac{b}{10}=\frac{3}{5}$，解得a = 3，b = 6，所以缩小后的直角三角形的面积为$\frac{1}{2}\times3\times6 = 9$。

14. 如图，已知在$Rt\triangle OAC$中，$O$为坐标原点，直角顶点$C$在$x$轴的正半轴上，反比例函数$y = \frac{k}{x}(k\neq0)$在第一象限的图象经过$OA$的中点$B$，交$AC$于点$D$，连接$OD$. 若$\triangle OCD\sim\triangle ACO$，则直线$OA$的解析式为__________.

答案： $y = 2x$ 设OC = a，因为点D在反比例函数$y=\frac{k}{x}$的图象上，所以$CD=\frac{k}{a}$。因为△OCD∽△ACO，所以$\frac{OC}{AC}=\frac{CD}{CO}$，所以$AC=\frac{OC^2}{CD}=\frac{a^2}{k}$，所以点A的坐标为$A(a,\frac{a^2}{k})$。因为B是OA的中点，所以点B的坐标为$(\frac{a}{2},\frac{a^2}{2k})$，因为点B在反比例函数$y=\frac{k}{x}$的图象上，所以$k=\frac{a}{2}\cdot\frac{a^2}{2k}$，所以$a^4 = 4k^2$，解得$a^2 = 2k$，所以点B的坐标为$(\frac{a}{2},a)$。设直线OA的解析式为$y = mx$，则$m\cdot\frac{a}{2}=a$，解得m = 2，所以直线OA的解析式为$y = 2x$。

15. 如图，$AB$与$CD$相交于点$O$，$\triangle OBD\sim\triangle OAC$，$\frac{OD}{OC}=\frac{3}{5}$，$OB = 6$，$S_{\triangle OAC}=50$. 求：
(1)$OA$的长；
(2)$S_{\triangle OBD}$.

答案： 解：（1）因为△OBD∽△OAC，所以$\frac{OB}{OA}=\frac{OD}{OC}=\frac{3}{5}$，因为OB = 6，所以OA = 10；（2）因为△OBD∽△OAC，且$\frac{OD}{OC}=\frac{3}{5}$，所以$\frac{S_{\triangle OBD}}{S_{\triangle OAC}}=\frac{9}{25}$，因为$S_{\triangle OAC}=50$，所以$S_{\triangle OBD}=18$。

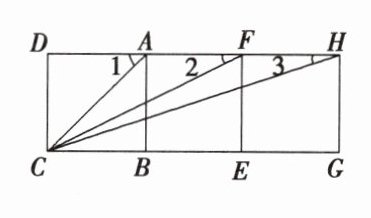
16. 如图所示，三个边长为$1$的正方形$ABCD$，$ABEF$，$EFHG$拼在一起.
(1)请找出图中相似的两个三角形，并证明；
(2)求$\angle1+\angle2+\angle3$这三个角度数之和.

答案： 解：（1）△ACF∽△AHC。证明如下：因为三个正方形的边长均为1，所以AD = CD = AF = 1，AH = 2，所以$AC=\sqrt{AD^2 + CD^2}=\sqrt{2}$，所以$\frac{AC}{AH}=\frac{AF}{AC}=\frac{\sqrt{2}}{2}$，又∠FAC = ∠CAH，所以△ACF∽△AHC；（2）因为△ACF∽△AHC，所以∠2 = ∠ACH，而∠1 = ∠ACH + ∠3，所以∠1 = ∠2 + ∠3。因为∠1 = 45°，所以∠1 + ∠2 + ∠3 = 90°。