第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
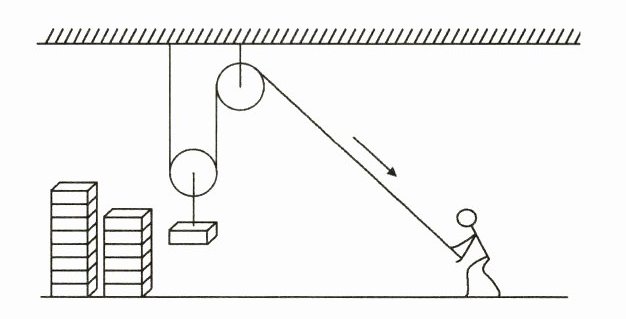
22. (14 分)某同学用如图所示的实验装置测量滑轮组的机械效率,相关数据记录在下表中.
|实验次数|钩码重/N|钩码上升的高度/m|绳端的拉力/N|绳端移动的距离/m|机械效率|
| ---- | ---- | ---- | ---- | ---- | ---- |
|1|4|0.1|1.8|0.3| |
|2|6|0.1|2.5|0.3| |
|3|6|0.15|2.5| | |
(1)实验中,使用滑轮组提升重物时,应竖直向上________拉动弹簧测力计.
(2)第 2 次实验中,2 s 内钩码上升的高度为 0.1 m,则它运动的速度为________ m/s.
(3)第 3 次实验中,绳端移动的距离为________ m,滑轮组的机械效率为________.
(4)分析比较第 1、2 两次实验的数据,有用功 W₍有用₎₁________W₍有用₎₂,滑轮组的机械效率 η₁________η₂(前两空均选填“>”“=”或“<”). 由此可知,可采用________的方法来提高滑轮组的机械效率.
|实验次数|钩码重/N|钩码上升的高度/m|绳端的拉力/N|绳端移动的距离/m|机械效率|
| ---- | ---- | ---- | ---- | ---- | ---- |
|1|4|0.1|1.8|0.3| |
|2|6|0.1|2.5|0.3| |
|3|6|0.15|2.5| | |
(1)实验中,使用滑轮组提升重物时,应竖直向上________拉动弹簧测力计.
(2)第 2 次实验中,2 s 内钩码上升的高度为 0.1 m,则它运动的速度为________ m/s.
(3)第 3 次实验中,绳端移动的距离为________ m,滑轮组的机械效率为________.
(4)分析比较第 1、2 两次实验的数据,有用功 W₍有用₎₁________W₍有用₎₂,滑轮组的机械效率 η₁________η₂(前两空均选填“>”“=”或“<”). 由此可知,可采用________的方法来提高滑轮组的机械效率.

答案:
(1)匀速
(2)0.05
(3)0.45 80%
(4)< < 增加物重
(1)匀速
(2)0.05
(3)0.45 80%
(4)< < 增加物重
四、计算题(6 分)
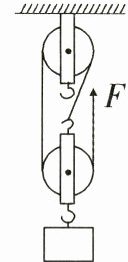
23. (6 分)建筑工地上,工人们需要将一堆建材运到 10 m 高处. 小董设计安装了如图所示的装置. 装置中每个滑轮重 100 N. 工人利用该装置每次匀速提升一块重 900 N 的建材,建材上升的速度是 0.6 m/s,在施工过程中,求:
(1)若不计绳重和摩擦,该装置的有用功的功率和机械效率.
(2)若不计绳重,绳子自由端拉力为 520 N 时,每次提升克服摩擦所做的功.
23. (6 分)建筑工地上,工人们需要将一堆建材运到 10 m 高处. 小董设计安装了如图所示的装置. 装置中每个滑轮重 100 N. 工人利用该装置每次匀速提升一块重 900 N 的建材,建材上升的速度是 0.6 m/s,在施工过程中,求:
(1)若不计绳重和摩擦,该装置的有用功的功率和机械效率.
(2)若不计绳重,绳子自由端拉力为 520 N 时,每次提升克服摩擦所做的功.

答案:
解:
(1)该装置的有用功的功率$P_{有用}=\frac{W_{有用}}{t}=\frac{Gh}{t}=Gv_{物}=900\ N\times0.6\ m/s = 540\ W$,因为不计绳重和摩擦,所以该装置的机械效率$\eta = \frac{W_{有用}}{W_{总}}\times100\% = \frac{W_{有用}}{W_{有用}+W_{额外}}\times100\% = \frac{Gh}{Gh + G_{动}h}\times100\% = \frac{G}{G + G_{动}}\times100\% = \frac{900\ N}{900\ N + 100\ N}\times100\% = 90\%$.
(2)由图可知$n = 2$,绳子自由端移动的距离$s = nh = 2\times10\ m = 20\ m$,则总功$W_{总}=Fs = 520\ N\times20\ m = 10 400\ J$,有用功$W_{有用}=Gh = 900\ N\times10\ m = 9 000\ J$,克服动滑轮重力做的额外功$W_{动}=G_{动}h = 100\ N\times10\ m = 1 000\ J$,所以每次提升克服摩擦做功$W_{f}=W_{总}-W_{有用}-W_{动}=10 400\ J - 9 000\ J - 1 000\ J = 400\ J$.
(1)该装置的有用功的功率$P_{有用}=\frac{W_{有用}}{t}=\frac{Gh}{t}=Gv_{物}=900\ N\times0.6\ m/s = 540\ W$,因为不计绳重和摩擦,所以该装置的机械效率$\eta = \frac{W_{有用}}{W_{总}}\times100\% = \frac{W_{有用}}{W_{有用}+W_{额外}}\times100\% = \frac{Gh}{Gh + G_{动}h}\times100\% = \frac{G}{G + G_{动}}\times100\% = \frac{900\ N}{900\ N + 100\ N}\times100\% = 90\%$.
(2)由图可知$n = 2$,绳子自由端移动的距离$s = nh = 2\times10\ m = 20\ m$,则总功$W_{总}=Fs = 520\ N\times20\ m = 10 400\ J$,有用功$W_{有用}=Gh = 900\ N\times10\ m = 9 000\ J$,克服动滑轮重力做的额外功$W_{动}=G_{动}h = 100\ N\times10\ m = 1 000\ J$,所以每次提升克服摩擦做功$W_{f}=W_{总}-W_{有用}-W_{动}=10 400\ J - 9 000\ J - 1 000\ J = 400\ J$.
查看更多完整答案,请扫码查看


