《2025年高中同步单元滚动强化卷高中物理选择性必修第二册人教版》

13. (9分)有一个教学用的可拆变压器，如图9甲所示，它有两个外观基本相同和粗细相同的同种导线绕成的线圈$ A $、$ B $，线圈外部还可以绕线。
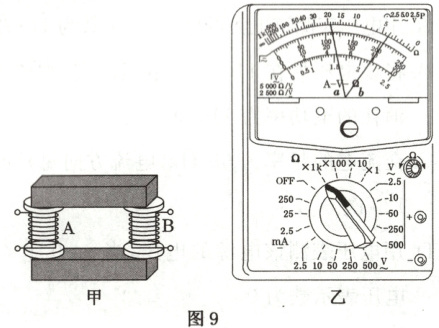
(1)某同学用一多用电表的同一欧姆挡先后测量了$ A $、$ B $线圈的电阻值，指针分别对应图9乙中的$ a $、$ b $位置($ a $在左、$ b $在右)，由此可推断A(填“$ A $”或“$ B $”)线圈的匝数较多。
(2)如果把它看成理想变压器，$ A $、$ B $线圈的匝数比为$ k $，则当$ A $线圈接在电压为$ U_1 $的蓄电池两端以后，$ B $线圈的输出电压为$\frac{U_{1}}{k}$。
(3)如果把它看成理想变压器，则$ A $、$ B $线圈上的交变电流一定具有相同的C(填字母)。
A. 电压
B. 电流
C. 功率
(4)现要测量$ A $线圈的匝数，提供的器材有：一根足够长的绝缘导线、一只多用电表和低压交流电源。实验步骤如下：
① 用长导线绕一个匝数为$ n $的线圈$ C $作为副线圈代替$ A $线圈；
② 把低压交流电源接在$ B $线圈上，测得$ C $线圈的输出电压为$ U $；
③ 用$ A $线圈换下$ C $线圈，测得$ A $线圈的输出电压为$ U_A $，则线圈$ A $的匝数$ n_A = $$\frac{U_{\mathrm{A}}}{U} n$(用物理量$ n $、$ U $、$ U_A $表示)。

答案： 13.解析:
(1)根据$R = \rho \frac{l}{S}$，从多用电表读数可知，指针a所指的电阻数值大于指针b所指的电阻数值，所以A线圈的匝数较多。
(2)根据变压器电压公式可知$\frac{U_{1}}{U_{2}} = k$，则$U_{2} = \frac{U_{1}}{k}$。
(3)理想变压器两端功率相同，所以A、B线圈上的交变电流一定具有相同的功率。故选C。
(4)根据变压器的电压比等于匝数之比，可知$\frac{U_{\mathrm{A}}}{U} = \frac{n_{\mathrm{A}}}{n}$，解得$n_{\mathrm{A}} = \frac{U_{\mathrm{A}}}{U} n$。
答案:
(1)A　
(2)$\frac{U_{1}}{k}$　
(3)C　
(4)$\frac{U_{\mathrm{A}}}{U} n$

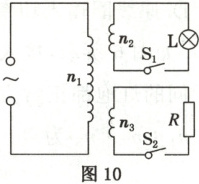
14. （9分）（2025·新乡模拟）如图10所示，理想变压器的原线圈连接峰值为$ 16 \sqrt{2} \mathrm{V} $的正弦式交流电，该变压器的原线圈$ n_1 = 800 $匝，副线圈$ n_2 $未知，$ n_3 = 200 $匝，两副线圈分别接上灯泡$ \mathrm{L} $和定值电阻$ R $。闭合开关$ \mathrm{S}_1 $，灯泡正常发光，已知灯泡的额定功率为$ 8 \mathrm{W} $，额定电流为$ 1 \mathrm{A} $，定值电阻$ R = 4 \Omega $。求：
（1）副线圈匝数$ n_2 $；
（2）若同时闭合开关$ \mathrm{S}_1 $和$ \mathrm{S}_2 $，原线圈中的电流$ I_1 $。

答案： 14.解析:
(1)灯泡正常发光，设灯泡两端的电压为$U_{2}$，对灯泡由电功率公式可得$P_{额} = U_{2} I_{额}$，解得$U_{2} = 8V$。原线圈的电压$U_{1} = \frac{U_{\mathrm{m}}}{\sqrt{2}} = 16V$，理想变压器原、副线圈的电压比等于匝数比，可得$\frac{U_{1}}{U_{2}} = \frac{n_{1}}{n_{2}}$，解得$n_{2} = 400$匝。
(2)若同时闭合开关$S_{1}$和$S_{2}$，设电阻$R$两端电压为$U_{3}$，对副线圈$n_{3}$则有$\frac{U_{1}}{U_{3}} = \frac{n_{1}}{n_{3}}$，解得$U_{3} = 4V$。对电阻$R$由电功率公式可得$P_{R} = \frac{U_{3}^{2}}{R} = 4W$。由理想变压器原、副线圈的功率相等可得$U_{1} I_{1} = P_{额} + P_{R}$，解得$I_{1} = 0.75A$。
答案:
(1)400匝　
(2)$0.75A$